题目内容
如图2 - 146所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.
(1)求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2 m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?

解:(1)设所求抛物线的解析式为y=ax2,设D(5,b),则B(10,b-3),把D,B的坐标分别代入y=ax2,得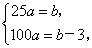 解得
解得 ∴y=-
∴y=-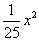 . (2)因为b=-1,所以
. (2)因为b=-1,所以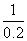 =5(小时).所以再持续5小时到达拱桥顶.
=5(小时).所以再持续5小时到达拱桥顶.

练习册系列答案
相关题目
某果品批发公司为指导今年的樱桃销售,对往年市场销售情况进行了调查统计,得到如下数据:
| 销售价x(元·千克-1) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
(1)在如图2 - 148所示的平面直角坐标系中,描出各组有序数对(x,y)所对应的点,连接各点并观察所得的图形.判断y与x之间的函数关系,并求出y与x之间的函数关系式;
(2)若樱桃进价为13元/千克.试求销售利润P(单位:元)与销售价x(单位:元/千克)之间的函数关系式,并求出当x取何值时,能获得最大利润?

 上.若OA=3,∠OCB=60°,∠1=∠2,则扇形OEF的面积为 .
上.若OA=3,∠OCB=60°,∠1=∠2,则扇形OEF的面积为 .
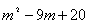 是二次函数,则m的值为 .
是二次函数,则m的值为 . cm B.
cm B. cm C.
cm C. cm D.
cm D. cm
cm
 ,∠D=30°.
,∠D=30°.