题目内容
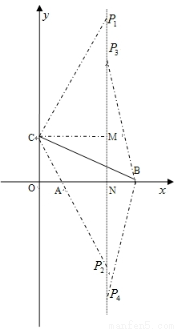
(本题12分)如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与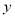 轴相切于点C,与
轴相切于点C,与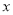 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线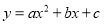 经过A,B,C三点.
经过A,B,C三点.
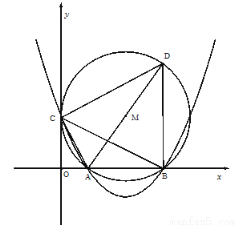
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)证明详见解析;(2)8;(3)存在,符合条件的点P有四个,坐标分别为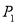
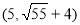 ,
,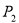
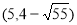 ,
,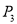
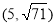 ,
,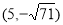 .
.
【解析】
试题分析:(1)利用切线的性质得出∠MCO=90°,进而得出∠OCA=∠MCD=∠MDC,再利用∠OCA+∠OAC=90°求出即可;
(2)利用圆周角定理以及平行线的性质,首先得出四边形COMN为矩形,进而求出BD=2MN;
(3)分别利用当CP=CB时,△PCB为等腰三角形,当BP=BC时,△PCB为等腰三角形,利用勾股定理求出即可.
试题解析:(1)证明:如图,连接MC,
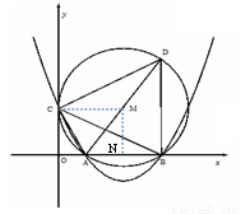
∵⊙M与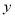 轴相切于点C,∴CM⊥OC,
轴相切于点C,∴CM⊥OC,
∴∠MCO=90°,
又∵∠ACD=90°,
∴AD为⊙M的直径,
∵DM=CM, ∠ACD+∠ADC=90°,
∴∠MCD=∠MDC,
∵∠OCA+∠ACM=∠OCM=90°,
∴∠MCD+∠ACM=90°,
∴∠OCA=∠MCD=∠MDC,
∵∠OCA+∠OAC=90°,
∴∠OAC=∠CAD;
(2)【解析】
如图,过点M作MN⊥OB于点N,
由(1)可知,AD是⊙M的直径,
∴∠ABD=90°,
∵MN⊥AB, ∴∠MNA=90°,
∴MN∥BD,
∴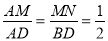 ,
,
∵∠OCM=∠CON=∠MNO=90°,
∴四边形COMN为矩形,
∴MN=CO=4,
∴BD=2MN=8;
(3)【解析】
抛物线的对称轴上存在点P,使ΔPBC是以BC为腰的等腰三角形.
在⊙M中,弧AC=弧AC,∴∠ADC=∠ABC,
由(1)知,∠ADC=∠OCA,
∴∠OCA=∠OBC,
在Rt△CAO和Rt△BOC中,tan∠OCA=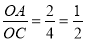 ,
,
∴tan∠OBC=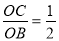 ,
,
∴OB=2OC=8,
∴A(2,0),B(8,0),
∵抛物线经过A,B两点,
∴A,B关于抛物线的对称轴对称,其对称轴为直线: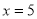 ;
;
当CP=CB=5时,△PCB为等腰三角形,
在Rt△COB中, ,
,
如图,在Rt△CM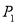 中,
中,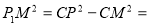 80-25=55,
80-25=55,
∴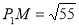 ,
,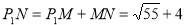
∴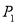
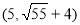 ,
,
同理可求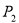 的坐标是
的坐标是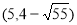 ,
,
当BP=BC=5时,△PCB为等腰三角形, ,
,
∴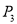
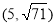 ,
,
同理可得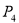 坐标为
坐标为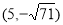 ,
,
∴符合条件的点P有四个,坐标分别为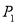
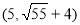 ,
,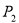
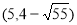 ,
,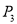
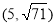 ,
,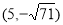 .
.
考点:二次函数综合题.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 阅读快车系列答案
阅读快车系列答案 ,要使
,要使 ≌
≌ ,应添加的条件是 (添上一个条件即可).
,应添加的条件是 (添上一个条件即可).
 +(y+2)2=0,则yx= .
+(y+2)2=0,则yx= . 有意义,则x应满足( ).
有意义,则x应满足( ).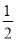 ≤x≤3 B.x≤3且x≠
≤x≤3 B.x≤3且x≠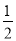 C.
C.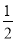 <x<3 D.
<x<3 D.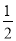 <x≤3
<x≤3 =
=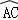 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
 的整数解是___________.
的整数解是___________.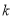 ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的
,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的 .
.
 为负数的概率;
为负数的概率;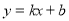 的图象经过二、三、四象限的概率。(用树状图或列表法求解)
的图象经过二、三、四象限的概率。(用树状图或列表法求解) .
.