题目内容
(本小题满分8分)有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的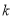 ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的
,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的 .
.

(1)写出 为负数的概率;
为负数的概率;
(2)求一次函数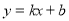 的图象经过二、三、四象限的概率。(用树状图或列表法求解)
的图象经过二、三、四象限的概率。(用树状图或列表法求解)
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)利用概率的计算方法解答;(2)由图表解答.
试题解析:【解析】
(1)因为共有3张牌,两张为负数,所以 为负数的概率是
为负数的概率是 ;
;
(2)画树状图或用列表法:
第二次 第一次 | -1 | -2 | 3 |
-1 | (-l,-2) | (-1,3) | |
-2 | (-2,-l) | (-2,3) | |
3 | (3,-l) | (3,-2) |
共有6种情况,其中满足一次函数 经过第二、三、四象限,即
经过第二、三、四象限,即 ,
, 的情况有2种,所以一次函数
的情况有2种,所以一次函数 经过第二、三、四象限的概率为
经过第二、三、四象限的概率为 .
.
考点:列表法或树状图法;概率公式;一次函数图象上点的坐标特点.
考点分析: 考点1:概率 用列表法或树形图解答的概率问题。 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 (
(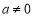 )的图象如图所示,对称轴为直线
)的图象如图所示,对称轴为直线 ,有下列结论:①
,有下列结论:① <0;②
<0;②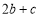 <0;③
<0;③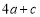 <
< .其中正确结论的个数是( )
.其中正确结论的个数是( )
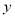 轴相切于点C,与
轴相切于点C,与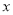 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线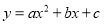 经过A,B,C三点.
经过A,B,C三点.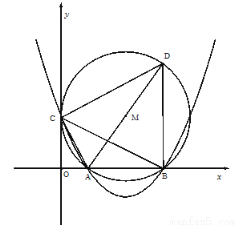
 的方程
的方程 ,下列说法正确的是( ).
,下列说法正确的是( ).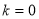 时,方程无解
时,方程无解  时,方程有两个相等的实数解
时,方程有两个相等的实数解 时,方程有一个实数解
时,方程有一个实数解 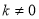 时,方程总有两个不相等的实数解
时,方程总有两个不相等的实数解 B.
B. C.
C. D.
D.

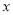 ,∠ACB=
,∠ACB= ,则
,则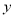 与
与 之间的关系是( ).
之间的关系是( ).
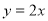 B.
B.
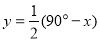 D.
D.