题目内容
18. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.(1)求反比例函数y=$\frac{m}{x}$和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
(3)当kx+b>$\frac{m}{x}$时,请写出自变量x的取值范围.
分析 (1)把A的坐标代入y=$\frac{m}{x}$求出m,即可得出反比例函数的表达式,把C的坐标代入y=$\frac{10}{x}$求出C的坐标,把A、C的坐标代入y=kx+b得出方程组,求出k、b,即可求出一次函数的表达式;
(2)把x=0代入y=x-3求出OB,分别求出△AOB和△BOC的面积,相加即可;
(3)根据A、C的坐标和图象得出即可.
解答 解:(1)把A﹙-2,-5﹚代入y=$\frac{m}{x}$得:m=10,
即反比例函数的表达式为y=$\frac{10}{x}$,
把C﹙5,n﹚代入y=$\frac{10}{x}$得:n=2,
即C(5,2),
把A、C的坐标代入y=kx+b得:$\left\{\begin{array}{l}{-2k+b=-5}\\{5k+b=2}\end{array}\right.$,
解得:k=1,b=-3,
所以一次函数的表达式为y=x-3;
(2)把x=0代入y=x-3得:y=-3,
即OB=3,
∵C(5,2),A﹙-2,-5﹚,
∴△AOC的面积为$\frac{1}{2}$×3×|-2|+$\frac{1}{2}$×3×5=10.5;
(3)由图象可知:当kx+b>$\frac{m}{x}$时,自变量x的取值范围是-2<x<0或x>5.
点评 本题考查了用待定系数法求一次函数和反比例函数的解析式,函数图象上点的坐标特征,函数的图象和性质的应用,能求出两函数的解析式是解此题的关键,数形结合思想的应用.

练习册系列答案
相关题目
13.化简
(1)-7mn+mn+5nm
(2)(2-m2+4m)-(5m2-m-1)
(3)(-3a2-2a)-[a2-2(5a-4a2+1)-3a]
(4)5x2-(3y2+7xy)+2(2y2-5x2)
(1)-7mn+mn+5nm
(2)(2-m2+4m)-(5m2-m-1)
(3)(-3a2-2a)-[a2-2(5a-4a2+1)-3a]
(4)5x2-(3y2+7xy)+2(2y2-5x2)
7. 某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:
某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:
单位:米
(1)求甲队身高的中位数;
(2)如果选拔标准是身高越整齐越好,那么甲乙两个队哪个队被录取?请说明理由.
 某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:
某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:单位:米
| 平均数 | 标准差 | 中位数 | |
| 甲队 | 1.72 | 0.038 | 1.73 |
| 乙队 | 1.69 | 0.025 | 1.70 |
(2)如果选拔标准是身高越整齐越好,那么甲乙两个队哪个队被录取?请说明理由.
8.下列各数中,最小的数是( )
| A. | -4 | B. | -2 | C. | 1 | D. | $\frac{1}{2}$ |
 如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=2DE,连接CF.判断四边形BCFE的形状,并证明.
如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=2DE,连接CF.判断四边形BCFE的形状,并证明.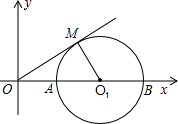 如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.