题目内容
6. 如图,在平面直角坐标系中,A(1,0),B(0,2),以AB为边在第一象限作正方形ABCD,点D恰好落在双曲线y=$\frac{k}{x}$上,则k的值是( )
如图,在平面直角坐标系中,A(1,0),B(0,2),以AB为边在第一象限作正方形ABCD,点D恰好落在双曲线y=$\frac{k}{x}$上,则k的值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 作DE⊥x轴于E,证明△AOB≌△DEA,根据全等三角形的性质得到AE=OB=2,DE=OA=1,求出点D的坐标,代入解析式计算即可.
解答 解: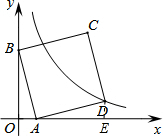 作DE⊥x轴于E,
作DE⊥x轴于E,
∵A(1,0),B(0,2),
∴OA=1,OB=2,
∵∠BAD=90°,∠AOB=90°,
∴∠ABO=∠DAE,
在△AOB和△DEA中,
$\left\{\begin{array}{l}{∠ABO=∠DAE}\\{∠AOB=∠DEA}\\{AB=AD}\end{array}\right.$,
∴△AOB≌△DEA,
∴AE=OB=2,DE=OA=1,
∴点D的坐标为(3;1),
∵点D恰好落在双曲线y=$\frac{k}{x}$上,
∴k=3,
故选:B.
点评 本题考查的是反比例函数图象上点的坐标特征、正方形的性质,反比例函数y=$\frac{k}{x}$图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
17.-$\frac{1}{5}$xay与-3x2yb-2是同类项,则a+b=( )
| A. | 6 | B. | 3 | C. | 5 | D. | 4 |
1.下列运算中,结果正确的是( )
| A. | 3a2+4a2=7a4 | B. | 4m2n+2mn2=6m2n | C. | 2x2-$\frac{1}{2}$x2=$\frac{3}{2}$x2 | D. | 2a-a=2 |

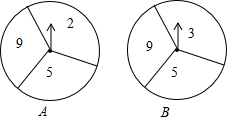 如图,有两个构造完全相同(除所标数字外)的转盘A,B,每个转盘都被分成3个大小相同的扇形,指针位置固定,游戏规定,转动两个转盘各一次,转盘停止后若A盘指针指示区域数字比B盘指针指示区域数字大则小明胜,否则小亮胜(指针指向两个扇形的交线时,当作指向右边的扇形).你认为这个游戏规则公平吗?为什么?
如图,有两个构造完全相同(除所标数字外)的转盘A,B,每个转盘都被分成3个大小相同的扇形,指针位置固定,游戏规定,转动两个转盘各一次,转盘停止后若A盘指针指示区域数字比B盘指针指示区域数字大则小明胜,否则小亮胜(指针指向两个扇形的交线时,当作指向右边的扇形).你认为这个游戏规则公平吗?为什么? 如图,在平面直角坐标系中,△ABC的顶点A(0,4),C(1,0),点B在第一象限,∠ACB=90°,AC=BC,则顶点B的坐标是(5,1).
如图,在平面直角坐标系中,△ABC的顶点A(0,4),C(1,0),点B在第一象限,∠ACB=90°,AC=BC,则顶点B的坐标是(5,1). 已知有理数m、n的和m+n与差m-n在数轴上如图所示,则化简|3m+n|-3|m|-|n-7|的值是-7.
已知有理数m、n的和m+n与差m-n在数轴上如图所示,则化简|3m+n|-3|m|-|n-7|的值是-7.