题目内容
4.若分式方程$\frac{1}{x-2}$+3=$\frac{b-x}{a+x}$有增根,则a的值是( )| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
分析 增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x-2)(a+x)=0,得到x=2或-a,然后代入化为整式方程的方程算出a的值.
解答 解:∵分式方程$\frac{1}{x-2}$+3=$\frac{b-x}{a+x}$有增根,
∴(x-2)(a+x)=0,
∴x=2或-a,
当x=2时,a=-2,
当x=-a时不合题意,
故选:D.
点评 本题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.某楼盘商品房成交价今年3月份为a元/m3,4月份比3月份减少了8%,若4月份到6月份平均增长率为12%,则6月份商品房成交价是( )
| A. | a(1-8%)(1+12%)元 | B. | a(1-8%)(1+12%)2元 | C. | (a-8%)(a+12%)元 | D. | a(1-8%+12%)元 |
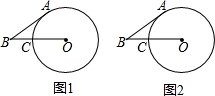 BA与⊙O相切,切点为A,连接OB交⊙O于点C.
BA与⊙O相切,切点为A,连接OB交⊙O于点C.
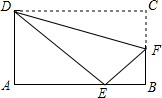 如图,将矩形ABCDE沿DF折叠,使点C落在AB的边上的点E处.
如图,将矩形ABCDE沿DF折叠,使点C落在AB的边上的点E处.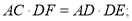
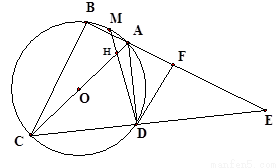
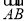 的中点,连接MD交弦AB于点H,若
的中点,连接MD交弦AB于点H,若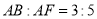 ,证明:
,证明: 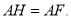
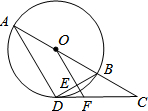 如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.
如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.