题目内容
7.某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下关系:| x | 3 | 5 |
| y | 18 | 14 |
(2)设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售规律:试求出日销售利润P元与日销售单价x元之间的函数表达式,并求出日销售单价x为多少元时,才能获得最大日销售利润?
分析 (1)根据题意设出销售量y件与日销售单价x元之间的函数表达式,然后根据题目中的数据即可求得函数解析式;
(2)根据题意和(1)中的函数解析式即可用含x的代数式表示出P,然后将P的关系式化为顶点式即可解答本题.
解答 解:(1)设销售量y件与日销售单价x元之间的函数表达式是y=kx+b,
$\left\{\begin{array}{l}{3k+b=18}\\{5k+b=14}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-2}\\{b=24}\end{array}\right.$,
∴销售量y件与日销售单价x元之间的函数表达式是y=-2x+24;
(2)由题意可得,
P=x(-2x+24)=-2x2+24x=-2(x-6)2+72,
∴日销售利润P元与日销售单价x元之间的函数表达式是P=-2x2+24x,当日销售单价x为6元时,才能获得最大日销售利润.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式,利用二次函数的顶点式求函数的最值.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为( )
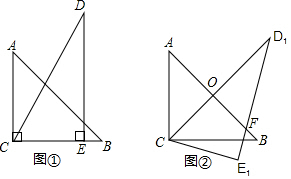

| A. | 10° | B. | 15° | C. | 7.5° | D. | 20° |
16.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 5cm,6cm,10cm | C. | 1cm,1cm,3cm | D. | 2cm,4cm,8cm |
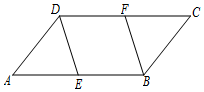 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF.