题目内容
8.点O在△ABC的内部,点D,E,F,G分别是AB,OB,OC,AC的中点.(1)如图1,求证:四边形DEFG是平行四边形;
(2)如图2,射线AO交BC边于点H,连接DH,GH,若AB=AC,DE⊥EF,在不添加任何辅助线的情况下,请直接写出图2中所有的等腰三角形(不包含以∠BAC为内角的三角形).

分析 (1)只要证明DG∥EF,DG=EF即可.
(2)首先证明AH垂直平分BC,得到△OBC,△OEF是等腰三角形,再根据直角三角形斜边中线性质得到△HGC,△HGA,△BDH,△DHA是等腰三角形.
解答 (1)证明:如图1中,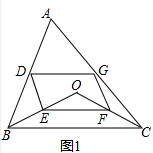
∵AD=DB,AG=GC,
∴DG∥BC,DG=$\frac{1}{2}$BC,
∵OE=EB,OF=FC,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴DG∥EF,EF=DG,
∴四边形DEFG是平行四边形.
(2)如图2中,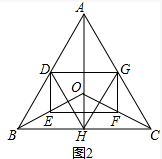
∵BD=DA,BE=EO,
∴DE∥AO,
∵EF∥BC,DE⊥EF,
∴DE⊥BC,
∴AH⊥BC,
∵AB=AC,
∴BH=HC,
∴OB=OC,OE=OF,
∴△OBC,△OEF是等腰三角形,
∵DH是RT△ABH斜边中线,
∴DH=BD=AD,
∴△BDH,△DHA是等腰三角形,同理△HGC,△HGA都是等腰三角形.
综上所述等腰三角形有△OBC,△OEF,△HGC,△HGA,△BDH,△DHA.
点评 本题考查三角形中位线性质,解题的关键是灵活应用三角形中位定理识解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.把长宽分别为7和4的长方形经过割补变为一个正方形,这个正方形的边长在( )
| A. | 5与6之间 | B. | 4与5之间 | C. | 3与4之间 | D. | 2与3之间 |
16.代数式x2+1,$\sqrt{x},|y|,{(m-1)^2},\root{3}{3}$中一定是正数的( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.直角三角形的一条直角边长为$\sqrt{2}$cm,斜边长为$\sqrt{10}$cm,则此三角形的面积为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
13.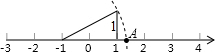 如图,数轴上的点A所表示的数为x,则x的值为( )
如图,数轴上的点A所表示的数为x,则x的值为( )
 如图,数轴上的点A所表示的数为x,则x的值为( )
如图,数轴上的点A所表示的数为x,则x的值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | $\sqrt{5}$-1 | D. | 1-$\sqrt{5}$ |
17.下列长度的三条线段:①3,8,4②4,9,6③15,20,8④9,15,8,其中能构成三角形的有( )
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
6.下列各数中,比1小的是( )
| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{3}{4}$ | D. | π |
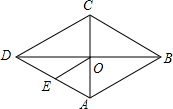 如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为32,则OE的长等于( )
如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为32,则OE的长等于( )