题目内容
20.若$\sqrt{x-3}$+(y-1)2=0,则x,y为边长的等腰三角形的周长为7.分析 首先利用非负数的性质可以得到x-3=0且y-1=0,进而求得x=3,y=1,然后分两种情况并运用三角形的三边关系进行解答即可.
解答 解:∵$\sqrt{x-3}$+(y-1)2=0,
∴x-3=0且y-1=0,
解得x=3,y=1,
当等腰三角形的腰为3时,三角形的三边为3,3,1,符合三角形的三边关系,此时三角形的周长为3+3+1=7;
当等腰三角形的腰为1时,三角形的三边为3,1,1,由于1+1<3,所以不符合三角形的三边关系,不能构成三角形;
所以x,y为边长的等腰三角形的周长为7.
故答案为:7.
点评 本题考查了非负数的性质,等腰三角形的性质,三角形的三边关系等知识,解答本题的关键是利用非负数的性质求出x与y的值,同时注意分类讨论思想的运用.

练习册系列答案
相关题目
8.如果不等式组$\left\{\begin{array}{l}4x-1>x+8\\ x>m\end{array}\right.$的解集是x>3,那么m的取值范围是( )
| A. | m>3 | B. | m>4 | C. | m≤4 | D. | m≤3 |
10.已知等腰三角形的顶角为40°,则这个等腰三角形的底角为( )
| A. | 40° | B. | 70° | C. | 100° | D. | 140° |
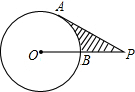 已知:如图,⊙O的半径为2,PA切⊙O于A,OP交⊙O于B,且PA=2$\sqrt{3}$,则阴影部分的面积S=2$\sqrt{3}$-$\frac{2}{3}$π.
已知:如图,⊙O的半径为2,PA切⊙O于A,OP交⊙O于B,且PA=2$\sqrt{3}$,则阴影部分的面积S=2$\sqrt{3}$-$\frac{2}{3}$π. 如图,AB是斜靠在墙角的长梯,梯角B距墙0.8m,长梯上一点D距墙0.7m,BD长0.55m,则梯子的长度是4.4m.
如图,AB是斜靠在墙角的长梯,梯角B距墙0.8m,长梯上一点D距墙0.7m,BD长0.55m,则梯子的长度是4.4m.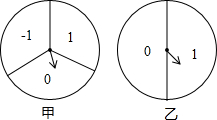 如图,分别转动甲、乙两个转盘各一次(指针落在每一数字区域的机会均等,若指针恰好落在分界线上则重转),当转盘停止时,把甲转盘指针指向的数字作为点A(x,y)的横坐标,把乙转盘指针指向的数字作为点A的纵坐标.
如图,分别转动甲、乙两个转盘各一次(指针落在每一数字区域的机会均等,若指针恰好落在分界线上则重转),当转盘停止时,把甲转盘指针指向的数字作为点A(x,y)的横坐标,把乙转盘指针指向的数字作为点A的纵坐标.