题目内容
如图，AE是圆O的直径，点B在AE的延长线上，点D在圆O上，且AC⊥DC，AD平分∠EAC（1）求证：BC是圆O的切线．
（2）若BE=8，BD=12，求圆O的半径．
考点：切线的判定
专题：
分析：（1）利用角平分线的性质以及等腰三角形的性质得出∠CAD=∠ADO，进而利用平行线的判定与性质得出∠ODB=90°，进而得出答案；
（2）利用切割线定理得出AB的长，即可得出答案．
（2）利用切割线定理得出AB的长，即可得出答案．
解答：
（1）证明：连接DO，
∵AD平分∠EAC，
∴∠CAD=∠DAO，
∵AO=DO，
∴∠DAO=∠ADO，
∴∠CAD=∠ADO，
∴AC∥DO，
∵∠C=90°，
∴∠ODB=90°，
∴BC是圆O的切线；
（2）解：∵BC是圆O的切线，
∴BE×BA=BD2，
∵BE=8，BD=12，
∴AB=
=18，
∴AE=18-8=10，
∴圆O的半径为：5．
（1）证明：连接DO，∵AD平分∠EAC，
∴∠CAD=∠DAO，
∵AO=DO，
∴∠DAO=∠ADO，
∴∠CAD=∠ADO，
∴AC∥DO，
∵∠C=90°，
∴∠ODB=90°，
∴BC是圆O的切线；
（2）解：∵BC是圆O的切线，
∴BE×BA=BD2，
∵BE=8，BD=12，
∴AB=
| 144 |
| 8 |
∴AE=18-8=10，
∴圆O的半径为：5．
点评：此题主要考查了切线的判定以及切割线定理，熟练掌握切割线定理是解题关键．
练习册系列答案
相关题目
|
A、±
| ||
B、±
| ||
C、
| ||
D、
|
（1）雅安地震牵动着全国人民的心，某单位开展了“一方有难，八方支援”赈灾捐款活动，第一天收到捐款10000元，第三天收到捐款12100元，如果第二天、第三天收到捐款的增长率相同，求捐款增长率？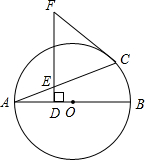
如图，AB是⊙O的直径，DF⊥AB于点D，交弦AC于点E，FC=FE．
如图，△ABC的两条高AD、CE相交于点H，D、E分别是垂足，过点C作BC的垂线交△ABC的外接圆于点F，求证：AH=FC．
如图是某市出租车单程收费y（元）与行驶路程x（千米）之间的函数关系图象，根据图象回答下列问题：