题目内容
7.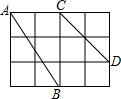 如图,在4×3正方形网格中,每个小正方形的边长都是1
如图,在4×3正方形网格中,每个小正方形的边长都是1(1)分别求出线段AB、CD的长度;
(2)在图中画线段EF、使得EF的长为$\sqrt{5}$,以AB、CD、EF三条线段能否构成直角三角形,并说明理由.
分析 (1)利用勾股定理求出AB、CD的长即可;
(2)根据勾股定理的逆定理,即可作出判断.
解答 解:(1)AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$;CD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
(2)如图,EF=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵CD2+EF2=8+5=13,AB2=13,
∴CD2+EF2=AB2,
∴以AB、CD、EF三条线可以组成直角三角形.
点评 本题考查了勾股定理、勾股定理的逆定理,充分利用网格是解题的关键.

练习册系列答案
相关题目
18.若一粒米的质量约是0.000023kg,将数据0.000023用科学记数法表示为( )
| A. | 23×104 | B. | 2.3×104 | C. | 2.3×105 | D. | 2.3×10-5 |
2. 实数a,b在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{(a-b)^{2}}$的结果是( )
 实数a,b在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{(a-b)^{2}}$的结果是( )
实数a,b在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{(a-b)^{2}}$的结果是( )| A. | -2b | B. | -2a | C. | 2(b-a) | D. | 0 |
12.若等腰三角形的两边长分别为3cm和6cm,则这个三角形的周长是( )
| A. | 12cm或15cm | B. | 15cm | C. | 12cm | D. | 9cm |
19. 如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记PA=x,点D到直线PA的距离为y,则y关于x的函数解析式是( )
如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记PA=x,点D到直线PA的距离为y,则y关于x的函数解析式是( )
 如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记PA=x,点D到直线PA的距离为y,则y关于x的函数解析式是( )
如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记PA=x,点D到直线PA的距离为y,则y关于x的函数解析式是( )| A. | y=12x | B. | $y=\frac{12}{x}$ | C. | $y=\frac{3}{4}x$ | D. | $y=\frac{4}{3}x$ |
16.下列样本的选取具有代表性的是( )
| A. | 利用某地七月份的日平均气温估计当地全年的日平均气温 | |
| B. | 为了解我国居民的年平均阅读时间,从大学生中随机抽取10万人进行抽查 | |
| C. | 调查某些七年级(1)班学生的身高;来估计该校全体学生的身高 | |
| D. | 为了了解一批洗衣粉的质量情况,从仓库中任意抽取100袋进行检验 |