题目内容
6.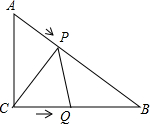 已知:Rt△ABC中,∠ACB=90°,CA=3,CB=4,设P,Q分别为AB边,CB边上的动点,它们同时分别从A,C出发,以每秒1个单位长度的速度向终点B运动,设P,Q运动的时间为t秒.
已知:Rt△ABC中,∠ACB=90°,CA=3,CB=4,设P,Q分别为AB边,CB边上的动点,它们同时分别从A,C出发,以每秒1个单位长度的速度向终点B运动,设P,Q运动的时间为t秒.(1)求△CPQ的面积S与运动时间t之间的函数关系式,并求出S的最大值.
(2)t为何值时,△CPQ为直角三角形.
(3)①探索:△CPQ是否可能为正三角形,说明理由.
②P,Q两点同时出发,若点P的运动速度不变,试改变点Q的运动速度,使△CPQ为正三角形,求出点Q的运动速度和此时的t值.
分析 (1)作PD⊥AC于D,PE⊥BC于E,根据勾股定理求出AB,用t表示出AD、PD,根据三角形的面积公式计算即可;
(2)根据勾股定理列出算式,求出t的值;
(3)①根据等边三角形的三线合一列式计算即可;
②设点Q的运动速度为a,根据等边三角形的性质列式求出a,根据等边三角形的性质、正切的概念计算即可.
解答 解:(1)作PD⊥AC于D,PE⊥BC于E,
∵∠ACB=90°,CA=3,CB=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵AP=t,
∴AD=$\frac{3}{5}$t,PD=$\frac{4}{5}$t,
∴PE=DC=3-$\frac{3}{5}$t,
∴S=$\frac{1}{2}$×t×(3-$\frac{3}{5}$t)=-$\frac{3}{10}$t2+$\frac{3}{2}$t,
∵S=-$\frac{3}{10}$t2+$\frac{3}{2}$t=-$\frac{3}{10}$(t-$\frac{5}{2}$)2+$\frac{15}{8}$,
∴S的最大值为$\frac{15}{8}$;
(2)只有当PC2+PQ2=CQ2时,△CPQ为直角三角形,
∴($\frac{4}{5}$t)2+(3-$\frac{3}{5}$t)2+(3-$\frac{3}{5}$t)2+(t-$\frac{4}{5}$t)2=t2,
解得,t1=3,t2=15(舍去),
∴当t=3时,△CPQ为直角三角形;
(3)①△CPQ不可能为正三角形,
理由如下:若△CPQ是正三角形,
则PC=PQ,EC=EQ,即t-$\frac{4}{5}$t=$\frac{4}{5}$t,
解得,t=0,
∴△CPQ不可能为正三角形;
②设点Q的运动速度为a,
当CE=EQ时,即$\frac{4}{5}$t=at-$\frac{4}{5}$t,
解得,a=$\frac{8}{5}$,
∵∠PCQ=60°,
∴PE=$\sqrt{3}$PD,
解得,t=$\frac{20\sqrt{3}-15}{13}$.
点评 本题考查的是直角三角形的性质、二次函数解析式的确定以及二次函数的性质的应用,掌握勾股定理、等边三角形的性质、灵活运用分情况讨论思想是解题的关键.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案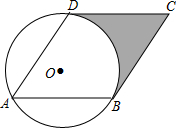 已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.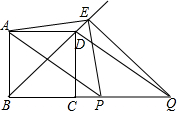 如图,BD是正方形ABCD的对角线,BC=2,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,同时动点Q从点C出发,以相同的速度沿射线BC运动,当点P出发后,过点Q作QE⊥BD,交直线BD于点E,连结AP、AE、PE、QE,设运动时间为t(秒).
如图,BD是正方形ABCD的对角线,BC=2,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,同时动点Q从点C出发,以相同的速度沿射线BC运动,当点P出发后,过点Q作QE⊥BD,交直线BD于点E,连结AP、AE、PE、QE,设运动时间为t(秒).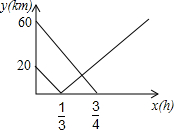 在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.
在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.