题目内容
4.平地上一棵树高为6米,两次观察地面上的影子,第一次是当阳光与地面成30°时,第二次是阳光与地面成60°时,第一次观察到的影子比第二次观察到的影子长( )| A. | 12-6$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 6-2$\sqrt{3}$ |
分析 如图,OA=6m,∠B=30°,∠ACO=60°,在Rt△AOB中利用正切定义可计算出OB=6$\sqrt{3}$,在Rt△AOC可计算出OC=2$\sqrt{3}$,然后计算OB-OC即可.
解答 解: 如图,OA=6m,∠B=30°,∠ACO=60°,
如图,OA=6m,∠B=30°,∠ACO=60°,
在Rt△AOB中,∵tanB=$\frac{OA}{OB}$,
∴OB=$\frac{6}{tan30°}$=6$\sqrt{3}$,
在Rt△AOC中,∵tan∠ACO=$\frac{OA}{OC}$,
∴OC=$\frac{6}{tan60°}$=2$\sqrt{3}$,
∴OB-OC=6$\sqrt{3}$-2$\sqrt{3}$=4$\sqrt{3}$(m).
故选B.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.也考查了解直角三角形.

练习册系列答案
相关题目
14. 如图,△ABC中,BC=1,B1、C1分别是AB、AC的中点,B2、C2分别是B1B、C1C的中点,B3、C3分别是B2B、C2C的中点,且B1C1=$\frac{1}{2}$,B2C2=$\frac{3}{4}$,B3C3=$\frac{7}{8}$,以此规律,线段B5C5的长为( )
如图,△ABC中,BC=1,B1、C1分别是AB、AC的中点,B2、C2分别是B1B、C1C的中点,B3、C3分别是B2B、C2C的中点,且B1C1=$\frac{1}{2}$,B2C2=$\frac{3}{4}$,B3C3=$\frac{7}{8}$,以此规律,线段B5C5的长为( )
 如图,△ABC中,BC=1,B1、C1分别是AB、AC的中点,B2、C2分别是B1B、C1C的中点,B3、C3分别是B2B、C2C的中点,且B1C1=$\frac{1}{2}$,B2C2=$\frac{3}{4}$,B3C3=$\frac{7}{8}$,以此规律,线段B5C5的长为( )
如图,△ABC中,BC=1,B1、C1分别是AB、AC的中点,B2、C2分别是B1B、C1C的中点,B3、C3分别是B2B、C2C的中点,且B1C1=$\frac{1}{2}$,B2C2=$\frac{3}{4}$,B3C3=$\frac{7}{8}$,以此规律,线段B5C5的长为( )| A. | $\frac{31}{32}$ | B. | $\frac{63}{64}$ | C. | $\frac{127}{128}$ | D. | 以上答案都不对 |
19.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\root{3}{2}$ | D. | $\sqrt{20}$ |
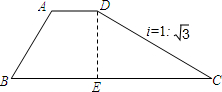 如图,梯形ABCD是拦水坝的横断面图,图中斜坡CD的坡度i=1:$\sqrt{3}$,∠B=60°,AB=6,AD=4,拦水坝的横断面ABCD的面积30$\sqrt{3}$.
如图,梯形ABCD是拦水坝的横断面图,图中斜坡CD的坡度i=1:$\sqrt{3}$,∠B=60°,AB=6,AD=4,拦水坝的横断面ABCD的面积30$\sqrt{3}$. 将两个直角三角形按图中方式叠放,则角α的度数等于75°.
将两个直角三角形按图中方式叠放,则角α的度数等于75°.
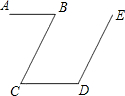 如图,直线AB∥CD,BC∥DE,若∠B=55°,则∠D=125°.
如图,直线AB∥CD,BC∥DE,若∠B=55°,则∠D=125°.