题目内容
8.边长为6的等边三角形面积等于9$\sqrt{3}$.分析 根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求三角形ABC的面积,即可解题.
解答 解:等边三角形高线即中线,故D为BC中点,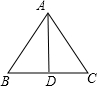
∵AB=6,
∴BD=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3$\sqrt{3}$,
∴等边△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$.
故答案为:9$\sqrt{3}$.
点评 本题考查了勾股定理在直角三角形中的运用,等边三角形面积的计算,本题中根据勾股定理计算AD的值是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
16.已知x=y,下列变形中不正确的是( )
| A. | x+5=y+5 | B. | 3-x=3-y | C. | ax=ay | D. | x-4=y+4 |
3.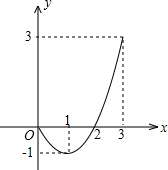 已知二次函数的图象(0≤x≤3)如图所示,下列关于该函数在所给自变量取值范围内的说法正确的是( )
已知二次函数的图象(0≤x≤3)如图所示,下列关于该函数在所给自变量取值范围内的说法正确的是( )
 已知二次函数的图象(0≤x≤3)如图所示,下列关于该函数在所给自变量取值范围内的说法正确的是( )
已知二次函数的图象(0≤x≤3)如图所示,下列关于该函数在所给自变量取值范围内的说法正确的是( )| A. | 有最小值0,最大值3 | B. | 有最小值-1,最大值3 | ||
| C. | 有最小值-1,最大值0 | D. | 有最小值-1,无最大值 |
13.下列各式的因式分解中正确的是( )
| A. | x2-xy+x=x(x-y) | B. | ax2-9=a(x+3)(x-3) | C. | x2-2x+4=x(x-2)+4 | D. | a2-2ab+b2=(a-b)2 |
18. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).| A. | ab | B. | 2ab | C. | a2-ab | D. | b2+ab |
 如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,线段PN的最小值是( )
如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,线段PN的最小值是( )