题目内容
19．
如图，若OP平分∠AOB，PM⊥OA于M点，PM=3，N是OB上一个动点，线段PN的最小值是（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 根据垂线段最短可得PN⊥OB时，PN最短，再根据角平分线上的点到角的两边距离相等可得PN=PM．
解答 解：由垂线段最短可得PN⊥OB时，PN最短，
∵OP平分∠AOB，PM⊥OA，
∴PN=PM=3，
即线段PN的最小值是3．
故选B．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，垂线段最短，熟记性质并判断出PN与OB垂直时PN的值最小是解题的关键．
练习册系列答案
相关题目
10．
如图，点D在线段AB上，且D是线段AB的中点，BD=4，则线段AB的长为（ ）
如图，点D在线段AB上，且D是线段AB的中点，BD=4，则线段AB的长为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
解不等式3（x-2）≤4x-3，并把它的解集在数轴上表示出来．
4．
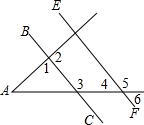如图，已知直线BC、EF分别与∠A的两边相交，且BC∥EF，则下列结论成立的是（ ）
如图，已知直线BC、EF分别与∠A的两边相交，且BC∥EF，则下列结论成立的是（ ）| A． | ∠2+∠5＞180° | B． | ∠2+∠3＜180° | C． | ∠1+∠6＞180° | D． | ∠3+∠4＜180° |