题目内容
19.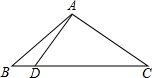 已知:如图,AB=AC=20,BC=32,D为BC边上一点,∠DAC=90°.求BD的长.
已知:如图,AB=AC=20,BC=32,D为BC边上一点,∠DAC=90°.求BD的长.
分析 作AM⊥BC于M,则BM=CM=16,利用△CAM∽△CDA得$\frac{CA}{CD}=\frac{CM}{CA}$,求出CD即可解决问题.
解答 解:如图作AM⊥BC于M.
∵AB=AC=20,BC=23,AM⊥BC,
∴BM=CM=16,
∵∠C=∠C,∠AMC=∠CAD,
∴△CAM∽△CDA,
∴$\frac{CA}{CD}=\frac{CM}{CA}$,
∴$\frac{20}{CD}$=$\frac{16}{20}$,
∴CD=25,
∴BD=BC-CD=32-25=7.
点评 本题考查相似三角形的性质、等腰三角形的性质等知识,解题的关键是添加辅助线构造相似三角形,记住等腰三角形中常用辅助线的添加方法,属于中考常考题型.

练习册系列答案
相关题目
10. 如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )
如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )
 如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )
如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )| A. | 若∠GAC=60°,则GH∥EF | B. | 若∠GAB=150°,则GH∥EF | ||
| C. | 若∠BAH=120°,则GH∥EF | D. | 若∠CAH=60°,则GH∥EF |
8.下列商标是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.下列方程中,有两个相等的实数根的是( )
| A. | x2-4x+4=0 | B. | x2-2x+5=0 | C. | x2-2x=0 | D. | x2-2x-1=0 |

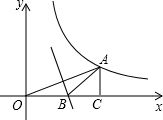 如图,点A在反比例函数y=$\frac{4}{x}$(x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为2$\sqrt{6}$.
如图,点A在反比例函数y=$\frac{4}{x}$(x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为2$\sqrt{6}$.