题目内容
18. 如图,O是线段AB上的点,且C,D分别是线段OA,OB的中点.
如图,O是线段AB上的点,且C,D分别是线段OA,OB的中点.(1)若AB=8,AO=6,求CD的长;
(2)若AB=a,O是线段AB上任意一点,试问CD的长又等于多少?(直接写出结果)
分析 (1)由AB=8,AO=6,得OB=2,所以CO=3,BO=1,可得CD的长;
(2)由图可看出AO+BO等于AB的长,已知,C,D分别是线段OA,OB的中点,所以CD即AB的一半.
解答 (1)解:∵AB=8,AO=6,
∴DO=2,
∵C,D分别是线段OA,OB的中点,
∴CO=3,BO=1,
∴CD=3+1=4;
(2)CD=$\frac{1}{2}$a;
证明:由图可看出AO+BO等于AB的长,
已知C,D分别是线段OA,OB的中点,
所以CD即AB的一半,
即CD=$\frac{1}{2}$a.
点评 本题考查了两点间的距离,线段的中点的定义,熟记线段中点的定义是解题的关键.

练习册系列答案
相关题目
6.我们把5个一元硬币摞在一起测得高度大约为1cm,那么10万个这样的硬币摞在一起,其高度最接近于( )
| A. | 地球赤道的长度 | B. | 地球半径的长度 | ||
| C. | 70层大厦的高度 | D. | 学校操场国旗旗杆的高度 |
10.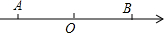 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )| A. | 2 | B. | x+5 | C. | -2 | D. | 4 |
8.七年级一班课外兴趣小组准备开会讨论问题,按如下方式摆放长书桌和椅子,发现一张长书桌边可以坐6个人,加一张长书桌时可以坐8个人,再加一张长书桌时可以坐10个人…

他们发现书桌和可坐人数数量变化有规律:(请把图表中的空格补充完整)

他们发现书桌和可坐人数数量变化有规律:(请把图表中的空格补充完整)
| 长桌张数 | 1 | 2 | 3 | 4 | … | n |
| 可坐人数 | 6 | 8 | 10 | 12 | … | 2n+4 |
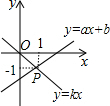 已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.