题目内容
7. 如图,在△ABC中∠ABC和∠ACB平分线交于点O,过点O作OD⊥BC于点D,△ABC的周长为18,OD=4,则△ABC的面积是36.
如图,在△ABC中∠ABC和∠ACB平分线交于点O,过点O作OD⊥BC于点D,△ABC的周长为18,OD=4,则△ABC的面积是36.
分析 作OE⊥AB于E,OF⊥AC于F,连接OA,根据角平分线的性质求出OE=OD=4和OF=OD=4,根据三角形面积公式计算即可.
解答 解: 作OE⊥AB于E,OF⊥AC于F,连接OA,
作OE⊥AB于E,OF⊥AC于F,连接OA,
∵OB是∠ABC的平分线,OD⊥BC,OE⊥AB,
∴OE=OD=4,
同理OF=OD=4,
△ABC的面积=$\frac{1}{2}$×AB×4+$\frac{1}{2}$×AC×4+$\frac{1}{2}$×BC×4=36.
点评 本题主要考查角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
2.正六边形的每个内角度数是( )
| A. | 60° | B. | 90° | C. | 108° | D. | 120° |
12. 如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )
如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )
 如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )
如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )| A. | 52° | B. | 38° | C. | 64° | D. | 26° |
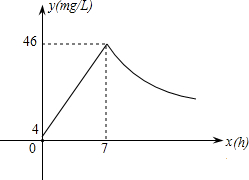 近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题:
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题: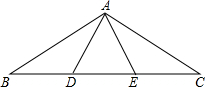 如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为120°.
如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为120°. 尺规作图(不写作法,保留作图痕迹)
尺规作图(不写作法,保留作图痕迹) 已知直角△ABC中,I为△ABC各内角平分线的交点,过I点作BC的垂线,垂足为H,若BC=6,AC=8,AB=10,那么IH的值为2.
已知直角△ABC中,I为△ABC各内角平分线的交点,过I点作BC的垂线,垂足为H,若BC=6,AC=8,AB=10,那么IH的值为2.