题目内容
19.已知多项式x-3x2ym+1+x3y-3x4-1是五次五项式,单项式3x3ny4-mz与多项式的次数相同,则mn=$\frac{4}{3}$.分析 利用多项式的次数定义得出m的值,进而利用单项式的次数得出n的值,即可得出答案.
解答 解:∵多项式x-3x2ym+1+x3y-3x4-1是五次四五项式,
∴2+m+1=5,
解得:m=2,
∵单项式3x3ny4-mz与多项式的次数相同,
∴3n+4-m+1=5,
解得:n=$\frac{2}{3}$,
∴mn=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 此题主要考查了多项式与单项式,正确把握多项式次数的定义是解题关键.

练习册系列答案
相关题目
7.已知:a-b=5,c+b=3,则(b+c)-(a-b)的值等于( )
| A. | -2 | B. | 2 | C. | 6 | D. | 8 |
4.计算(-2x+3y)(2x-3y)的结果为( )
| A. | -4x2+12xy-9y2 | B. | 4x2-9y2 | C. | 4x2-12xy+9y2 | D. | 9y2-4x2 |
8.下列各组式子中为同类项的是( )
| A. | 5x2y与-2xy2 | B. | 4x与4x2 | C. | $-3{x^2}y与\frac{1}{3}y{x^2}$ | D. | 6x4y2与-6x4z2 |
 如图,E、F分别为?ABCD的边AD、BC的中点,G、H在BD上,且BG=DH.求证:四边形EGFH是平行四边形.
如图,E、F分别为?ABCD的边AD、BC的中点,G、H在BD上,且BG=DH.求证:四边形EGFH是平行四边形.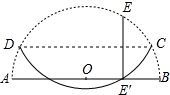 如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.
如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.