题目内容
11．
如图，BD是∠ABC的平分线，AD=CD．求证：∠DAB+∠BCD=180°．
分析 作DE⊥BA于E，DF⊥BC于F，根据角平分线的性质得到DE=DF，证明Rt△ADE≌Rt△CDF，得到∠DAE=∠DCB，根据邻补角的性质证明结论．
解答 证明：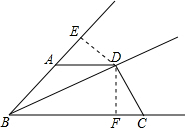
作DE⊥BA于E，DF⊥BC于F，
∵BD是∠ABC的平分线，DE⊥BA，DF⊥BC，
∴DE=DF，
在Rt△ADE和Rt△CDF中，
$\left\{\begin{array}{l}{AD=CD}\\{DE=DF}\end{array}\right.$，
∴Rt△ADE≌Rt△CDF，
∴∠DAE=∠DCB，
∵∠DAB+∠DAE=180°，
∴∠DAB+∠BCD=180°．
点评 本题考查的是角平分线的性质和直角三角形全等判定，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
相关题目
如图，△ABC中，∠B=∠C，D、E、F分别是BC、AB、AC上的点，且∠EDF=∠B，BE=CD，图中是否存在与△BDE全等的三角形？理由是什么？