题目内容
(本题满分10分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
【解析】
试题分析:(1)由OD⊥AC ,OD为半径,根据垂径定理,即可得 =
= ,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
试题解析:(1)∵OD⊥AC OD为半径,
∴  =
= .
.
∴∠CBD=∠ABD。
∴BD平分∠ABC.
(2)∵OB=OD,∠ODB=30°,
∴∠OBD=∠ODB=30°.
∴∠AOD=∠OBD+∠ODB=30°+30°=60°.
又∵OD⊥AC于E,
∴∠OEA=90°.
∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°.
∴在Rt△ACB中,BC= AB .
AB .
∵OD= AB,
AB,
∴BC=OD.
考点:垂径定理, 圆周角定理

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
 有最______点,其坐标是__________.
有最______点,其坐标是__________. +
+
 的正方形,长方形AEFG的宽
的正方形,长方形AEFG的宽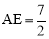 ,长
,长 .将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
 的度数;
的度数;
 是等腰直角三角形,
是等腰直角三角形, 是斜边,将
是斜边,将 绕点
绕点 逆时针旋转后,能与
逆时针旋转后,能与 重合,如果
重合,如果 ,那么
,那么 的长等于( )
的长等于( )
 (B)
(B) (C)
(C) (D)
(D)
 ,当两个三角形重叠的面积为32时,它移动的距离
,当两个三角形重叠的面积为32时,它移动的距离 等于 .
等于 .
