题目内容
如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△ ,当两个三角形重叠的面积为32时,它移动的距离
,当两个三角形重叠的面积为32时,它移动的距离 等于 .
等于 .

4或8
【解析】
试题分析:根据平移的性质,结合阴影部分是平行四边形,△AA′H与△HCB′都是等腰直角三角形,则若设AA′=x,则阴影部分的底长为x,高A′D=2-x,根据平行四边形的面积公式即可列出方程求解.
设AC交A′B′于H,
∵∠A=45°,∠D=90°
∴△A′HA是等腰直角三角形
设AA′=x,则阴影部分的底长为x,高A′D=12-x
∴x•(12-x)=32
∴x=4或8,
即AA′=4或8cm.
故答案为:4或8.
考点:1.平移的性质;2.解一元二次方程-因式分解法;3.平行四边形的判定与性质;4.正方形的性质

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目

 的图象如图所示.
的图象如图所示.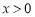 时,
时, 的取值范围
的取值范围
 中的自变量
中的自变量 的取值范围是( ).
的取值范围是( ). (B)
(B) (C)
(C) (D)
(D) 且
且



 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;