题目内容
研究表明一种培育后能繁殖的细胞在一定的环境下有以下规律:若有n个细胞,经过第一周期后,在第1个周期内要死去1个,会新繁殖(n-1)个;经过第二周期后,在第2个周期内要死去2个,又会新繁殖(n-2)个;以此类推.例如,细胞经过第x个周期后时,在第x个周期内要死去x个,又会新繁殖(n-x)个.
| 周期序号 | 在第x周期后细胞总数 |
| 1 | n-1+(n-1)=2(n-1) |
| 2 | 2(n-1)-2+(n-2)=3(n-2) |
| 3 | 3(n-2)-3+(n-3)=4(n-3) |
| … | … |
(Ⅱ)当n=21时,细胞在第________周期后时细胞的总个数最多,最多是________个.
y=(x+1)(n-x) 10 121
分析:(Ⅰ)细胞总个数y=(周期序号+1)×(n-周期序号);
(Ⅱ)把n=21代入(Ⅰ)得到的关系式,得到二次函数,利用公式法求得二次函数的最值即可.
解答:(Ⅰ)观察表格可得细胞总个数y=(周期序号+1)×(n-周期序号)
即y=(x+1)(n-x).
故答案为y=(x+1)(n-x);
(Ⅱ)当n=21时,y=(x+1)(21-x),
∴x=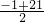 =10时,y最大=11×11=121.
=10时,y最大=11×11=121.
故答案为10,121.
点评:考查二次函数的相关知识;根据所给规律判断出y与x的关系是解决本题的突破点;判断出抛物线的对称轴解决最值问题简单且不易出差错.
分析:(Ⅰ)细胞总个数y=(周期序号+1)×(n-周期序号);
(Ⅱ)把n=21代入(Ⅰ)得到的关系式,得到二次函数,利用公式法求得二次函数的最值即可.
解答:(Ⅰ)观察表格可得细胞总个数y=(周期序号+1)×(n-周期序号)
即y=(x+1)(n-x).
故答案为y=(x+1)(n-x);
(Ⅱ)当n=21时,y=(x+1)(21-x),
∴x=
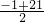 =10时,y最大=11×11=121.
=10时,y最大=11×11=121.故答案为10,121.
点评:考查二次函数的相关知识;根据所给规律判断出y与x的关系是解决本题的突破点;判断出抛物线的对称轴解决最值问题简单且不易出差错.

练习册系列答案
相关题目
研究表明一种培育后能繁殖的细胞在一定的环境下有以下规律:若有n 个细胞,经过第一周期后,在第1 个周期内要死去1个,会新繁殖(n-1)个;经过第二周期后,在第2 个周期内要死去2个,又会新繁殖(n-2)个;以此类推.例如, 细胞经过第x 个周期后时,在第x 个周期内要死去x个,又会新繁殖 (n-x)个。
|
周期序号 |
在第x周期后细胞总数 |
|
1 |
n-1+(n-1)=2(n-1) |
|
2 |
2(n-1)-2+(n-2)=3(n-2) |
|
3 |
3(n-2)-3+(n-3)=4(n-3) |
|
4 |
|
|
5 |
|
|
…… |
…… |
(1)根据题意,分别填写上表第4、5两个周期后的细胞总数;
(2)根据上表,直接写出在第x周期后时,该细胞的总个数y(用x、n表示);
(3)当n=21时,细胞在第几周期后时细胞的总个数最多?最多是多少个?

 个细胞,经过第一周期后,在第1 个周期内要死
个细胞,经过第一周期后,在第1 个周期内要死 去1个,会新繁殖(
去1个,会新繁殖( )个;经过第二周期后,在第2 个周期内要死去2个,又会新繁殖(
)个;经过第二周期后,在第2 个周期内要死去2个,又会新繁殖( )个;以此类推.例如, 细胞经过第
)个;以此类推.例如, 细胞经过第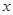 个周期后时
个周期后时 ,在第
,在第 )个.
)个.
 ,则
,则