题目内容
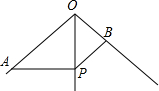 如图,OP平分∠AOB,且∠OAP+∠OBP=180°.求证:PA=PB.
如图,OP平分∠AOB,且∠OAP+∠OBP=180°.求证:PA=PB.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:作PM⊥OA,PN⊥OB交OA,OB于M,N,由OP为角平分线,利用角平分线定理得到PM=PN,由已知两角互补,以及邻补角定义得到一对角相等,再由一对直角相等,且PM=PN,利用AAS得到三角形PMA与三角形PNB全等,利用全等三角形对应边相等即可得证.
解答: 证明:作PM⊥OA,PN⊥OB交OA,OB于M,N,
证明:作PM⊥OA,PN⊥OB交OA,OB于M,N,
∵∠AOP=∠POB,
∴PM=PN,
∵∠OBP+∠OAP=180°,∠OBP+∠PBN=180°,
∴∠MAP=∠NBP,
在△PMA和△PNB中,
,
∴△PMA≌△PNB(AAS),
∴PA=PB.
 证明:作PM⊥OA,PN⊥OB交OA,OB于M,N,
证明:作PM⊥OA,PN⊥OB交OA,OB于M,N,∵∠AOP=∠POB,
∴PM=PN,
∵∠OBP+∠OAP=180°,∠OBP+∠PBN=180°,
∴∠MAP=∠NBP,
在△PMA和△PNB中,
|
∴△PMA≌△PNB(AAS),
∴PA=PB.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对于方程组
,把(2)代入(1)得( )
|
| A、2x-6x-1=5 |
| B、2(2x-1)-3y=5 |
| C、2x-6x+3=5 |
| D、2x-6x-3=5 |
 如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE
如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE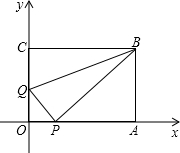 如图,在平面直角坐标系中,长方形OABC的两边分别在x轴和y轴上,且OA=14个单位长度,OC=8个单位长度,现有两个动点,P、Q,分别从O、C同时出发,P在线段OA上且以速度为1个单位长度/秒匀速运动,Q在线段CO上以0.5个单位长度/秒匀速运动,当其中一点到达线段的终点时,另一点也随之停止运动,设运动时间为t秒(t>0).
如图,在平面直角坐标系中,长方形OABC的两边分别在x轴和y轴上,且OA=14个单位长度,OC=8个单位长度,现有两个动点,P、Q,分别从O、C同时出发,P在线段OA上且以速度为1个单位长度/秒匀速运动,Q在线段CO上以0.5个单位长度/秒匀速运动,当其中一点到达线段的终点时,另一点也随之停止运动,设运动时间为t秒(t>0).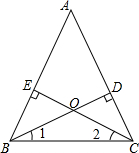 如图,如果BD⊥AC,CE⊥AB,CE与BD相交于点O,并且BO=CO,那么∠1=∠2.如果把上面的命题中的“BO=CO”改为结论,把“∠1=∠2”移入条件,所得到的命题还是否正确?请给出证明.
如图,如果BD⊥AC,CE⊥AB,CE与BD相交于点O,并且BO=CO,那么∠1=∠2.如果把上面的命题中的“BO=CO”改为结论,把“∠1=∠2”移入条件,所得到的命题还是否正确?请给出证明.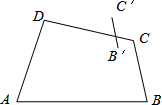 如图所示,已知四边形ABCD和线段B′C′,且线段BC与线段B′C′是位似图形.
如图所示,已知四边形ABCD和线段B′C′,且线段BC与线段B′C′是位似图形.