题目内容
 (2012•东莞)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(2012•东莞)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
分析:(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;
(2)由(1)可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=
AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
(2)由(1)可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=
| 1 |
| 2 |
解答:(1)证明:∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵
,
∴△ABG≌△C′DG;
(2)解:∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,设AG=x,则GB=8-x,
在Rt△ABG中,
∵AB2+AG2=BG2,即62+x2=(8-x)2,解得x=
,
∴tan∠ABG=
=
=
;
(3)解:∵△AEF是△DEF翻折而成,
∴EF垂直平分AD,
∴HD=
AD=4,
∴tan∠ABG=tan∠ADE=
,
∴EH=HD×
=4×
=
,
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF=
AB=
×6=3,
∴EF=EH+HF=
+3=
.
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵
|
∴△ABG≌△C′DG;
(2)解:∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,设AG=x,则GB=8-x,
在Rt△ABG中,
∵AB2+AG2=BG2,即62+x2=(8-x)2,解得x=
| 7 |
| 4 |
∴tan∠ABG=
| AG |
| AB |
| ||
| 6 |
| 7 |
| 24 |
(3)解:∵△AEF是△DEF翻折而成,
∴EF垂直平分AD,
∴HD=
| 1 |
| 2 |
∴tan∠ABG=tan∠ADE=
| 7 |
| 24 |
∴EH=HD×
| 7 |
| 24 |
| 7 |
| 24 |
| 7 |
| 6 |
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=EH+HF=
| 7 |
| 6 |
| 25 |
| 6 |
点评:本题考查的是翻折变换、全等三角形的判定与性质、矩形的性质及解直角三角形,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
相关题目
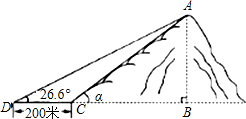 (2012•东莞)如图,小山岗的斜坡AC的坡度是tanα=
(2012•东莞)如图,小山岗的斜坡AC的坡度是tanα= (2012•东莞)如图,直线y=2x-6与反比例函数y=
(2012•东莞)如图,直线y=2x-6与反比例函数y=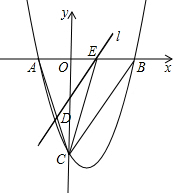 (2012•东莞)如图,抛物线y=
(2012•东莞)如图,抛物线y=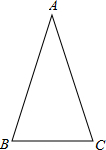 (2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.
(2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.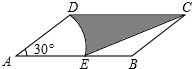 (2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是
(2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是