题目内容
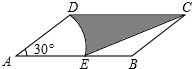 (2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是
(2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是3-
π
| 1 |
| 3 |
3-
π
(结果保留π).| 1 |
| 3 |
分析:过D点作DF⊥AB于点F.可求?ABCD和△BCE的高,观察图形可知阴影部分的面积=?ABCD的面积-扇形ADE的面积-△BCE的面积,计算即可求解.
解答: 解:过D点作DF⊥AB于点F.
解:过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD•sin30°=1,EB=AB-AE=2,
∴阴影部分的面积:
4×1-
-2×1÷2
=4-
π-1
=3-
π.
故答案为:3-
π.
 解:过D点作DF⊥AB于点F.
解:过D点作DF⊥AB于点F.∵AD=2,AB=4,∠A=30°,
∴DF=AD•sin30°=1,EB=AB-AE=2,
∴阴影部分的面积:
4×1-
| 30×π×22 |
| 360 |
=4-
| 1 |
| 3 |
=3-
| 1 |
| 3 |
故答案为:3-
| 1 |
| 3 |
点评:考查了平行四边形的性质,扇形面积的计算,本题的关键是理解阴影部分的面积=?ABCD的面积-扇形ADE的面积-△BCE的面积.

练习册系列答案
相关题目
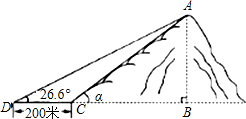 (2012•东莞)如图,小山岗的斜坡AC的坡度是tanα=
(2012•东莞)如图,小山岗的斜坡AC的坡度是tanα= (2012•东莞)如图,直线y=2x-6与反比例函数y=
(2012•东莞)如图,直线y=2x-6与反比例函数y=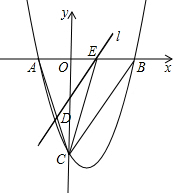 (2012•东莞)如图,抛物线y=
(2012•东莞)如图,抛物线y=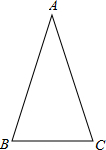 (2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.
(2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.