题目内容
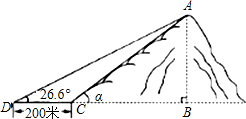 (2012•东莞)如图,小山岗的斜坡AC的坡度是tanα=
(2012•东莞)如图,小山岗的斜坡AC的坡度是tanα=| 3 | 4 |
分析:首先在直角三角形ABC中根据坡角的正切值用AB表示出BC,然后在直角三角形DBA中用BA表示出BD,根据BD与BC之间的关系列出方程求解即可.
解答:解:∵在直角三角形ABC中,
=tanα=
,
∴BC=
∵在直角三角形ADB中,
∴
=tan26.6°=0.50
即:BD=2AB
∵BD-BC=CD=200
∴2AB-
AB=200
解得:AB=300米,
答:小山岗的高度为300米.
| AB |
| BC |
| 3 |
| 4 |
∴BC=
| 4AB |
| 3 |
∵在直角三角形ADB中,
∴
| AB |
| BD |
即:BD=2AB
∵BD-BC=CD=200
∴2AB-
| 4 |
| 3 |
解得:AB=300米,
答:小山岗的高度为300米.
点评:本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2012•东莞)如图,直线y=2x-6与反比例函数y=
(2012•东莞)如图,直线y=2x-6与反比例函数y=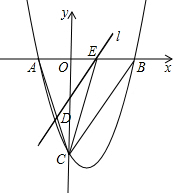 (2012•东莞)如图,抛物线y=
(2012•东莞)如图,抛物线y=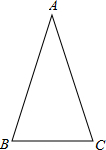 (2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.
(2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.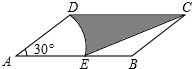 (2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是
(2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是