题目内容
抛物线y=x2-x+m,若其顶点在x轴上,则m= .
考点:二次函数的性质
专题:
分析:把抛物线方程化为顶点式,令其纵坐标为0即可求得m.
解答:解:∵y=x2-x+m=(x-
)2+m-
,
∴其顶点坐标为(
,m-
),
∵顶点在x轴上,
∴m-
=0,解得m=
.
故答案为:
.
| 1 |
| 2 |
| 1 |
| 4 |
∴其顶点坐标为(
| 1 |
| 2 |
| 1 |
| 4 |
∵顶点在x轴上,
∴m-
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题主要考查二次函数的顶点坐标,掌握二次函数的顶点式是解题的关键.

练习册系列答案
相关题目
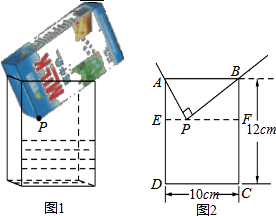 将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度.
将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度.