题目内容
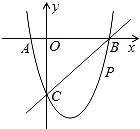
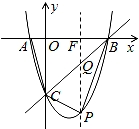
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
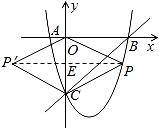
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;
(3)由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
【解答】解:(1)将B、C两点的坐标代入得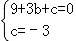 ,
,
解得: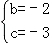 ;
;
所以二次函数的表达式为:y=x2﹣2x﹣3
(2)存在点P,使四边形POP′C为菱形;
设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E
若四边形POP′C是菱形,则有PC=PO;
连接PP′,则PE⊥CO于E,
∵C(0,﹣3),
∴CO=3,
又∵OE=EC,
∴OE=EC=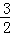
∴y=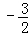 ;
;
∴x2﹣2x﹣3=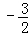
解得x1=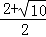 ,x2=
,x2=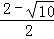 (不合题意,舍去),
(不合题意,舍去),
∴P点的坐标为(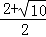 ,
,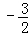 )
)
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3),设直线BC的解析式为:y=kx+d,
则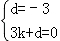 ,
,
解得: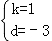
∴直线BC的解析式为y=x﹣3,
则Q点的坐标为(x,x﹣3);
当0=x2﹣2x﹣3,
解得:x1=﹣1,x2=3,
∴AO=1,AB=4,
S四边形ABPC=S△ABC+S△BPQ+S△CPQ
= AB•OC+
AB•OC+ QP•BF+
QP•BF+ QP•OF
QP•OF
=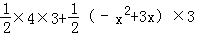
=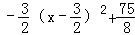
当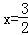 时,四边形ABPC的面积最大
时,四边形ABPC的面积最大
此时P点的坐标为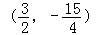 ,四边形ABPC的面积的最大值为
,四边形ABPC的面积的最大值为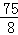 .
.
【点评】此题考查了二次函数解析式的确定、菱形的判定和性质以及图形面积的求法等知识,当所求图形不规则时通常要将其转换为其他规则图形面积的和差关系来求解.

 阅读快车系列答案
阅读快车系列答案
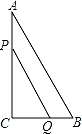
 中,自变量
中,自变量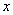 的取值范围在数轴上可表示为( )
的取值范围在数轴上可表示为( )
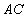 是底面圆的直径,高
是底面圆的直径,高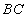 = 6cm,点
= 6cm,点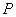 是母线
是母线 =
=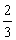
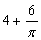 )cm B.5cm C.
)cm B.5cm C. cm D.7cm
cm D.7cm
 的结果是( )
的结果是( ) B.
B. C.﹣
C.﹣ ,且
,且 、
、 为连续正整数,则
为连续正整数,则 = .
= .