题目内容
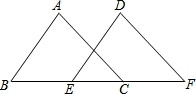
如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a(a<8)个单位到△DEF的位置.
(1)求△ABC的BC边上的高;
(2)连结AE、AD,设AB=5.
①求线段DF的长;
②当△ADE是等腰三角形时,求a的值.
【考点】等腰三角形的判定与性质;勾股定理;平移的性质.
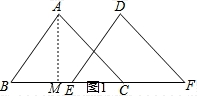
【分析】(1)如图1过点A作AM⊥BC于点M,由三角形的面积公式求得△ABC的BC边上的高是8;
(2)①在Rt△AMB中,由勾股定理求得BM=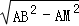 =
=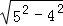 =3,得到CM=BC﹣BM=8﹣3=5,在Rt△AMC中,由勾股定理求得AC=
=3,得到CM=BC﹣BM=8﹣3=5,在Rt△AMC中,由勾股定理求得AC=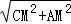 =
=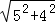 =
=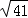 ,得到DF=AC=
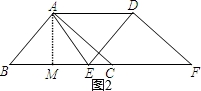
,得到DF=AC=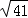 ;②如图2当△ADE是等腰三角形时,分三种情况讨论:当AD=DE时,a=5,当AE=DE时,因为AB=DE,得到AB=AE,BE=2BM=6,求得a=6;当AE=AD时,在Rt△AME中,AM=4,AE=a,ME=a﹣3,由勾股定理得:42+(a﹣3)2=a2,解得:a=
;②如图2当△ADE是等腰三角形时,分三种情况讨论:当AD=DE时,a=5,当AE=DE时,因为AB=DE,得到AB=AE,BE=2BM=6,求得a=6;当AE=AD时,在Rt△AME中,AM=4,AE=a,ME=a﹣3,由勾股定理得:42+(a﹣3)2=a2,解得:a=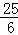 ,
,
【解答】解:(1)如图1过点A作AM⊥BC于点M,
∵△ABC的面积为16,BC=8,
∴ ×8×AM=8,∴AM=4,
×8×AM=8,∴AM=4,
∴△ABC的BC边上的高是8;
(2)①在Rt△AMB中,BM= =
=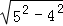 =3,
=3,
∴CM=BC﹣BM=8﹣3=5,
∴在Rt△AMC中,AC=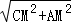 =
=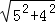 =
=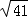 ,
,
∴DF=AC=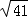 ,
,
②如图2当△ADE是等腰三角形时,有三种情况:
当AD=DE时,a=5,
当AE=DE时,又∵AB=DE,
∴AB=AE,
∴BE=2BM=6,∴a=6;
当AE=AD时,在Rt△AME中,
AM=4,AE=a,ME=a﹣3,
由勾股定理得:42+(a﹣3)2=a2,
解得:a=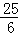 ,
,
综上所述,当△ADE是等腰三角形时,a的值为5或6或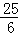 .
.
【点评】本题考查了等腰三角形的判定和性质,平移的性质,勾股定理得应用,特别是(2)②要分类讨论否则容易漏解.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案 ∠BAE=30°
∠BAE=30°