题目内容
3.某次初中数学竞赛试题中,有16道5分题和10道7分题,满分为150分.批改时每道题若答对得满分,答错得0分,没有其它分值.(1)如果晓敏同学答对了m道7分题和n道5分题,恰好得分为70分,列出关于m、n的方程,并写出这个方程符合实际意义的所有的解.
(2)假设某同学这份竞赛试卷的得分为k(0≤k≤150),那么k的值有多少种不同大小?请直接写出答案.
分析 (1)根据总分=分值×答对题目数即可得出7m+5n=70,即m=10-$\frac{5}{7}$n,再根据m、n均为非负整数,即可得出二元一次方程的解;
(2)设答对x道5分题和答对y道7分题时分数相等,即5x=7y,解之即可得出x、y的值,利用k=16×10-重复种数即可求出结论.
解答 解:(1)根据题意得:7m+5n=70,
∴m=10-$\frac{5}{7}$n.
∵m、n均为非负整数,
∴n=0时,m=10;n=7时,m=5;n=14时,m=0,
∴这个方程符合实际意义的所有的解为:$\left\{\begin{array}{l}{m=0}\\{n=14}\end{array}\right.$,$\left\{\begin{array}{l}{m=5}\\{n=7}\end{array}\right.$,$\left\{\begin{array}{l}{m=10}\\{n=0}\end{array}\right.$;
(2)设答对x道5分题和答对y道7分题时分数相等,
则5x=7y,
当x=7时,y=5;当x=14时,y=10.
∴当y=5时,重复的分数有16-7+1=10(种);当x=7时,重复的分数有10-5=5(种);当y=10时,重复的分数有16-7+1+16-14+1=13(种);当x=14时,重复的分数有10-5+10-10=5(种);
∴16×10-10-5-13-5=127(种).
∴k的值有127种不同大小.
点评 本题考查了二元一次方程的应用以及排列与组合问题,解题的关键是:(1)根据m、n的取值范围结合7m+5n=70找出所以可能解;(2)利用排列和组合的知识找出分值相等的重复次数.

练习册系列答案
相关题目
17.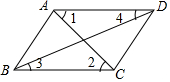 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )
 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )| A. | ∠BAD+∠ABC=180° | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠BAD=∠BCD |
15.某老师在试卷分析中说:参加这次考试的41位同学中,考121分的人数最多,虽然最高的同学获得了满分150分,但是十分遗憾最低的同学仍然只得了56分,其中分数居第21位的同学获得116分.这说明本次考试分数的中位数是( )
| A. | 21 | B. | 103 | C. | 116 | D. | 121 |
2.以下列各组线段为边,能组成三角形的是( )
| A. | 2,2,4 | B. | 2,3,6 | C. | 1,2,3 | D. | 3,4,5 |
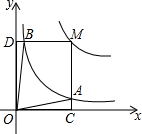 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.