题目内容
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() ,且对称轴为直线
,且对称轴为直线![]() .
.
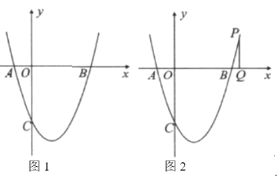
(1)求该抛物线的解析式;
(2)点![]() 是第四象限内抛物线上的一点,当
是第四象限内抛物线上的一点,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)如图2,点![]() 是抛物线上的一个动点,过点
是抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .当
.当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
![]() (3)
(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)由对称性可知抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 为
为![]() ,将点
,将点![]() ,
,![]() 坐标代入,联立方程组求解即可得到
坐标代入,联立方程组求解即可得到![]() ,即可得到抛物线的解析式.
,即可得到抛物线的解析式.
(2)作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设直线BC:y=kx+b,代入B、C两点坐标求得直线
,设直线BC:y=kx+b,代入B、C两点坐标求得直线![]() 为
为![]() ,设点
,设点![]() 为
为![]() ,则点
,则点![]() 为
为![]() ,
,![]() ,表示出S
,表示出S![]() ,化简整理可得
,化简整理可得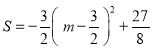 ,根据二次函数的性质得当
,根据二次函数的性质得当![]() 时,
时,![]() 的面积最大,此时点
的面积最大,此时点![]() 坐标为
坐标为![]()
(3)根据A、B 坐标易得AB=4,当PQ=3时满足条件,P点的纵坐标为±3,代入函数解析式求得P点的横坐标,即可得到P点的坐标.
解:(1)由对称性可知抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 为
为![]()
把点![]() ,
,![]() 坐标代入,
坐标代入,![]() ,解得
,解得![]()
抛物线的解析式为![]() .
.
(2)如图1,作![]() 轴交直线
轴交直线![]() 于点
于点![]()
设直线BC:y=kx+b,
代入B(3,0),C(0,-3)可得![]()
解得:![]()
∴直线![]() 为
为![]()
设点![]() 为
为![]() 则点
则点![]() 为
为![]()
![]()
![]()
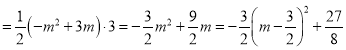
![]() 当
当![]() 时,
时,![]() 的面积最大,
的面积最大,
代入![]() ,可得
,可得![]() =
=![]() ,
,
此时点![]() 坐标为
坐标为![]()
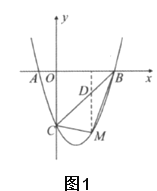
(3)∵A(-1,0),B(3,0)
∴AB=4
∵![]()
∴PQ=3,
即P点纵坐标为±3,
当y=3时,![]()
解得:![]()
当y=-3时,![]()
解得:x1=0,x2=2,
综上,当![]() 时,
时,![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目