题目内容
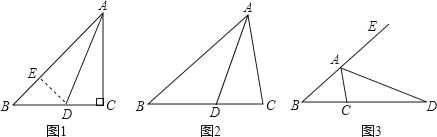
【题目】如图,在锐角![]() 中,
中,![]() 是
是![]() 边上的高.
边上的高. ![]() ,且
,且![]()
![]() .连接
.连接![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定正确的个数是( )
.其中一定正确的个数是( )

A.![]() 个B.
个B.![]() 个
个
C.![]() 个D.
个D.![]() 个
个
【答案】A
【解析】
首先根据题意,可得出∠FAE+∠BAD=90°,∠GAE+∠CAD=90°,进而得出∠FAE+∠BAD+∠GAE+∠CAD=180°,可判定①结论正确;由∠BAF+∠BAC=∠CAG+∠BAC,![]() ,得出∠FAC=∠BAG,
,得出∠FAC=∠BAG,![]()
![]() ,判定△FAC≌△BAG,判定②结论正确;由∠EAF+∠BAD=90°,∠BAD+∠ABC=90°,得出∠EAF=∠ABC,可判定④结论正确;由∠AFC=∠ABG,∠AFC+∠FHA=90°,对顶角相等,得出∠ABG+∠BHC=90°,即可判定③结论正确;故正确的结论有4个.
,判定△FAC≌△BAG,判定②结论正确;由∠EAF+∠BAD=90°,∠BAD+∠ABC=90°,得出∠EAF=∠ABC,可判定④结论正确;由∠AFC=∠ABG,∠AFC+∠FHA=90°,对顶角相等,得出∠ABG+∠BHC=90°,即可判定③结论正确;故正确的结论有4个.
解:∵![]() 是
是![]() 边上的高.
边上的高. ![]() ,
,
∴∠FAE+∠BAD=90°,∠GAE+∠CAD=90°
∴∠FAE+∠BAD+∠GAE+∠CAD=180°
∴![]() ,①结论正确;
,①结论正确;
∵![]()
∴∠BAF+∠BAC=∠CAG+∠BAC
∴∠FAC=∠BAG
又∵![]()
![]()
∴△FAC≌△BAG(SAS)
∴BG=CF,②结论正确;
∵∠EAF+∠BAD=90°,∠BAD+∠ABC=90°
∴∠EAF=∠ABC,④结论正确;
令CF和AB、BG分别交于点H、I
∵△FAC≌△BAG
∴∠AFC=∠ABG
又∵∠AFC+∠FHA=90°,∠FHA=∠BHC(对顶角相等)
∴∠ABG+∠BHC=90°,即∠BIF=90°,即![]() ,
,
③结论正确;正确的个数有4个.
故选:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
合计 | ________ | 1 |

根据上述信息,解答下列问题:
(1)这次书法作品比赛成绩的调查是采用_____(填“普查”或“抽样调查”),样本是_____.
(2)完成上表,并补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级奖的数量.