题目内容
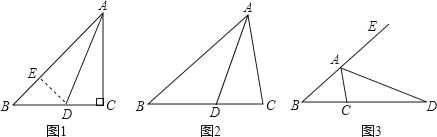
【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
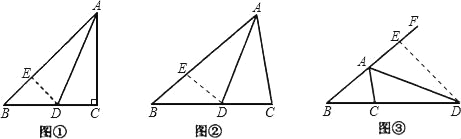
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
【答案】(1)猜想:AB=AC+CD(2)猜想:AB+AC=CD.
【解析】试题分析:(1)首先在AB上截取AE=AC,连接DE,易证△ADE≌△ADC(SAS),则可得∠AED=∠C,ED=CD,又由∠AED=∠ACB,∠ACB=2∠B,所以∠AED=2∠B,即∠B=∠BDE,易证DE=CD,则可求得AB=AC+CD;
(2)首先在BA的延长线上截取AE=AC,连接ED,易证△EAD≌△CAD,可得ED=CD,∠AED=∠ACD,又由∠ACB=2∠B,易证DE=EB,则可求得AC+AB=CD.
试题解析:(1)猜想:AB=AC+CD.
证明:如图②,在AB上截取AE=AC,连接DE,
∵AD为∠BAC的角平分线时,
∴∠BAD=∠CAD,
∵AD=AD,
∴△ADE≌△ADC(SAS),
∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴EB=ED,
∴EB=CD,
∴AB=AE+DE=AC+CD.
(2)猜想:AB+AC=CD.
证明:在BA的延长线上截取AE=AC,连接ED.
∵AD平分∠FAC,
∴∠EAD=∠CAD.
在△EAD与△CAD中,
AE=AC,∠EAD=∠CAD,AD=AD,
∴△EAD≌△CAD(SAS).
∴ED=CD,∠AED=∠ACD.
∴∠FED=∠ACB,
又∵∠ACB=2∠B
∴∠FED=2∠B,∠FED=∠B+∠EDB,
∴∠EDB=∠B,
∴EB=ED.
∴EA+AB=EB=ED=CD.
∴AC+AB=CD.

 寒假学与练系列答案
寒假学与练系列答案【题目】某中学举行“汉字听写”比赛,每位学生听写汉字![]() 个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
组别 | 正确字数 | 人数 |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|


(1)在统计表中,![]() ,
,![]() ;
;
(2)补全条形统计图;
(3)在扇形统计图中“D组”所对应的圆心角的度数为 ;
(4)若该校共有![]() 名学生,如果听写正确的字数少于
名学生,如果听写正确的字数少于![]() 个定为不合格,请你估计这所中学这次比赛听写不合格的学生人数.
个定为不合格,请你估计这所中学这次比赛听写不合格的学生人数.
【题目】某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.
经过调查,得到如下数据:
销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
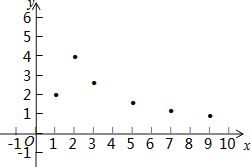
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系式,并求出函数关系式.
(2)物价部门规定,该工艺品的销售单价最高不超过45元/件,当销售单价x定为多少时,工艺厂试销该工艺品每天获得的利润8000元?(利润=销售总价﹣成本总价)
(3)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)