Question

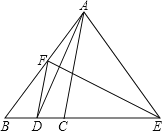
【题目】如图，E是正方形ABCD的边AB上的动点，但始终保持EF⊥DE交BC于点F．

（1）求证：△ADE∽△BEF；

（2）若正方形的边长为4，设AE=x，BF=y，求y与x之间的函数解析式；

（3）当x取何值时，y有最大值？并求出这个最大值．

Answer 1

【答案】（1）证明见解析；（2） ；（3）当时， 取得最大值， .

【解析】试题分析：（1）根据正方形的性质及余角的性质得出△ADE与△BEF的两对应角相等，从而得出△ADE∽△BEF；
（2）根据相似三角形的性质得出y关于x的函数解析式及函数的定义域；
（3）利用配方法，即可解决问题；

试题解析：

（1）∵ 四边形ABCD是正方形，

∴ ∠A＝∠B＝90°，∴ ∠1＋∠2＝90°，

又∵，∴ ∠2＋∠3＝90°，∴ ∠1＝∠3 ，

∴ ∽；

（2）依题意知：AB＝AD＝4，

∵，∴ BE＝ ，

由（1）知∽， ∴ ，

即 ，

∴ ，

即 ；

（3）∵ ，

∴ 当时， 取得最大值， .