题目内容
4.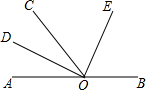 如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.(1)∠AOD的余角是∠COE、∠BOE,∠COD的余角是∠COE、∠BOE
(2 )OE是∠BOC的平分线吗?请说明理由.
分析 (1)直接利用角平分线的定义得出∠AOD=∠COD,进而利用已知得出∠AOD、∠COD的余角;
(2)利用(1)中所求得出OE是∠BOC的平分线.
解答 解:(1)∵OD平分∠AOC,
∴∠AOD=∠COD,
∵∠DOE=90°,
∴∠DOC+∠COE=90°,∠AOD+∠BOE=90°,
∴∠AOD+∠COE=90°,
∴∠AOD的余角是:∠COE、∠BOE;
∠COD的余角是:∠COE,∠BOE;
故答案为:∠COE,∠BOE;∠COE,∠BOE;
(2)OE平分∠BOC,
理由:∵∠DOE=90°,
∴∠AOD+∠BOE=90°,
∴∠COD+∠DOE=90°,
∴∠AOD+∠BOE=∠COD+∠DOE
∵OD平分∠AOC,
∴∠AOD=∠COD,
∴∠COE=∠BOE
∴OE平分∠BOC.
点评 此题主要考查了余角以及角平分线的定义,正确把握角平分线的定义是解题关键.

练习册系列答案
相关题目
15.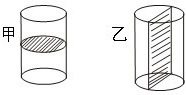 图是甲、乙两位同学对同一个圆柱的两种不同的切分方法(平均分成两块),这个圆柱的底面半径为1cm,高为4cm.甲切分后表面积增加了6.28cm2,乙切分后表面积增加了16cm2 (π≈3.14).
图是甲、乙两位同学对同一个圆柱的两种不同的切分方法(平均分成两块),这个圆柱的底面半径为1cm,高为4cm.甲切分后表面积增加了6.28cm2,乙切分后表面积增加了16cm2 (π≈3.14).
 图是甲、乙两位同学对同一个圆柱的两种不同的切分方法(平均分成两块),这个圆柱的底面半径为1cm,高为4cm.甲切分后表面积增加了6.28cm2,乙切分后表面积增加了16cm2 (π≈3.14).
图是甲、乙两位同学对同一个圆柱的两种不同的切分方法(平均分成两块),这个圆柱的底面半径为1cm,高为4cm.甲切分后表面积增加了6.28cm2,乙切分后表面积增加了16cm2 (π≈3.14).
12. 如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d相交于点O,若∠1=40°,则∠2等于( )
如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d相交于点O,若∠1=40°,则∠2等于( )
 如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d相交于点O,若∠1=40°,则∠2等于( )
如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d相交于点O,若∠1=40°,则∠2等于( )| A. | 140° | B. | 130° | C. | 120° | D. | 80° |
9.下列说法中错误的有( )
①n棱柱有n个面,2n个顶点,3n条棱;
②用一个平面截圆锥,截面可能是三角形;
③有公共点的两个直角组成平角;
④如果线段AB=BC,则点B是线段AC的中点.
①n棱柱有n个面,2n个顶点,3n条棱;
②用一个平面截圆锥,截面可能是三角形;
③有公共点的两个直角组成平角;
④如果线段AB=BC,则点B是线段AC的中点.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔10元,而按原定价的九折出售,每件将赚38元,则这种商品的原定价是( )
| A. | 200元 | B. | 240元 | C. | 320元 | D. | 360元 |
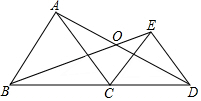 如图,△ABC与△ECD都是等边三角形,AB≠EC,下列结论中:①BE=AD;②∠BOD=120°;③OA=OD.正确的序号是①②.
如图,△ABC与△ECD都是等边三角形,AB≠EC,下列结论中:①BE=AD;②∠BOD=120°;③OA=OD.正确的序号是①②.
