题目内容
5.定义运算“※”为:a※b=$\left\{\begin{array}{l}a{b^2}(b>0)\\-a{b^2}(b≤0)\end{array}$,如:1※(-2)=-1×(-2)2=-4.则函数y=2※x的图象大致是( )| A. | 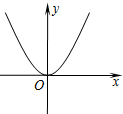 | B. | 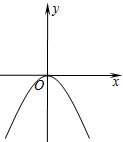 | C. | 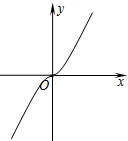 | D. | 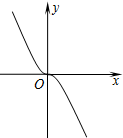 |
分析 根据定义运算“※”为:a※b=$\left\{\begin{array}{l}a{b^2}(b>0)\\-a{b^2}(b≤0)\end{array}$,可得y=2※x的函数解析式,根据函数解析式,可得函数图象.
解答 解:y=2※x=$\left\{\begin{array}{l}{2{x}^{2}(x>0)}\\{-2{x}^{2}(x≤0)}\end{array}\right.$,
x>0时,图象是y=2x2对称轴右侧的部分;x≤0时,图象是y=-x2对称轴左侧的部分,
故选:C.
点评 本题考查了二次函数的图象,利用定义运算“※”为:a※b=$\left\{\begin{array}{l}a{b^2}(b>0)\\-a{b^2}(b≤0)\end{array}$得出分段函数是解题关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
16.已知一次函数y=kx+2经过点(1,0),则k的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
14.已知二次函数y=x2+2x-k,小聪利用计算器列出了下表:
那么方程x2+2x-k=0的一个近似根是( )
| x | -4.1 | -4.2 | -4.3 | -4.4 |
| x2+2x-k | -1.39 | -0.76 | -0.11 | 0.56 |
| A. | -4.1 | B. | -4.2 | C. | -4.3 | D. | -4.4 |
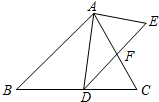 如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.
如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.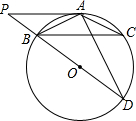 如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.
如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.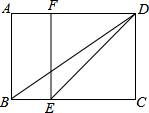 已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.
已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.