题目内容
3.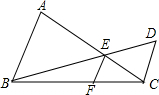 如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:
如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:(1)$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$;
(2)$\frac{1}{{S}_{△ABC}}+\frac{1}{{S}_{△DBC}}=\frac{1}{{S}_{△EBC}}$.
分析 (1)由AB∥EF∥CD,得到△CEF∽△CAB,△BEF∽BDC,根据相似三角形的性质得到$\frac{EF}{AB}=\frac{FC}{BC}$①,②,化简即可得到结论;
(2)分别作AM⊥BC于M,EN⊥BC于N,DG⊥BC于G,得到AM∥EN∥DG,根据相似三角形的性质结论得到结论.
解答 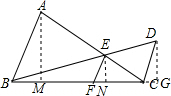 证明:(1)∵AB∥EF∥CD,
证明:(1)∵AB∥EF∥CD,
∴△CEF∽△CAB,△BEF∽BDC,
∴$\frac{EF}{AB}=\frac{FC}{BC}$①,②,
①+②得$\frac{EF}{AB}=\frac{FC}{BC}$①,
①+②得$\frac{EF}{AB}+\frac{EF}{CD}=\frac{FC+BF}{BC}$=1,
∴$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$;
(2)分别作AM⊥BC于M,EN⊥BC于N,DG⊥BC于G,
∴AM∥EN∥DG,
由(1)知$\frac{1}{AM}+\frac{1}{DG}=\frac{1}{EN}$,
∴$\frac{EN}{AM}+\frac{EN}{DG}=1$,
$\frac{{S}_{△EBC}}{{S}_{△ABC}}+\frac{{\;}_{△EBC}}{{S}_{△DBE}}$=$\frac{\frac{1}{2}BC•EN}{\frac{1}{2}BC•AM}+\frac{\frac{1}{2}BC•EN}{\frac{1}{2}BC•DG}$=$\frac{EN}{AM}+\frac{EN}{DG}$=1,
∴$\frac{1}{{S}_{△ABC}}+\frac{1}{{S}_{△DBC}}=\frac{1}{{S}_{△EBC}}$.
点评 本题考查了相似三角形的判定和性质,正确的作出辅助线是解题的关键.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | 9 | B. | 10 | C. | 11 | D. | 10或11 |
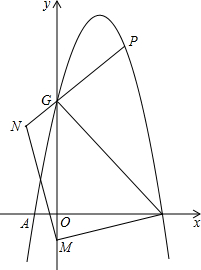 抛物线y=-x2+3x+4与x轴交于A,B两点,与y轴交于点C,如图,点M为y轴负半轴上一动点,点N在y轴左侧,MN⊥MB,MN=MB,连接NC交抛物线于点P,求点P的坐标.
抛物线y=-x2+3x+4与x轴交于A,B两点,与y轴交于点C,如图,点M为y轴负半轴上一动点,点N在y轴左侧,MN⊥MB,MN=MB,连接NC交抛物线于点P,求点P的坐标.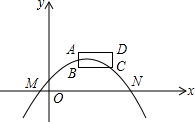 如图,矩形ABCD在平面直角坐标系的第一象限内,BC∥x轴,AB=1,BC=2,点B的坐标为(2,1),抛物线y=ax2+bx+c(a≠0)的顶点总是在矩形ABCD内部(包括边界),且与x轴的两个交点分别是点M(x1,0)、N(x2、0),其中-2≤x1≤-1,下列说法:①abc<0;②2a+b≤0;③当k<1时,方程ax2+bx+c-k=0总有两个不相等的实数根;④a的取值范围是-$\frac{2}{9}≤a≤-\frac{1}{36}$;其中正确的是①③④.
如图,矩形ABCD在平面直角坐标系的第一象限内,BC∥x轴,AB=1,BC=2,点B的坐标为(2,1),抛物线y=ax2+bx+c(a≠0)的顶点总是在矩形ABCD内部(包括边界),且与x轴的两个交点分别是点M(x1,0)、N(x2、0),其中-2≤x1≤-1,下列说法:①abc<0;②2a+b≤0;③当k<1时,方程ax2+bx+c-k=0总有两个不相等的实数根;④a的取值范围是-$\frac{2}{9}≤a≤-\frac{1}{36}$;其中正确的是①③④.
 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2.
如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2. 如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点且BD=2CD,连接AD并延长至E,使得AD=DE,求证:BE=$\frac{1}{2}$AE.
如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点且BD=2CD,连接AD并延长至E,使得AD=DE,求证:BE=$\frac{1}{2}$AE.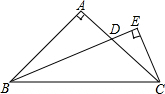 如图,△ABC中,AB=AC,∠BAC=90°,D是AC上一点,且CE⊥BD于点E,CE=$\frac{1}{2}$BD,求证:BD平分∠ABC.
如图,△ABC中,AB=AC,∠BAC=90°,D是AC上一点,且CE⊥BD于点E,CE=$\frac{1}{2}$BD,求证:BD平分∠ABC.