题目内容
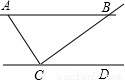
3.已知,OA=OC,OB=OD,∠AOC=∠B0D,直线AB、CD相交于P.①如图1,若∠AOC=∠BOD=90°,则∠APD=90°,并证明;
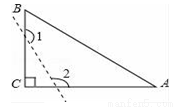
②如图2,若∠AOC=∠BOD=60°,则∠APD=120°,并证明.
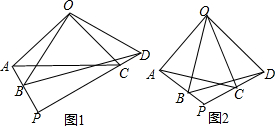
分析 (1)根据已知条件得到∠1=∠2,证得△OAB≌△OCD,根据全等三角形的性质得到∠OBA=∠ODC,于是得到∠PBD=180°-∠ABO-∠OBD=180°-45°-∠ODC=180°-45°-45°-∠BOP=90°-∠BDP,证得∠PBD+∠BOP=90°,即可得到结论;
(2)同(1)得到∠ABO=∠CDO,求得∠PBD=180°-∠ABO-∠OBD=180°-∠CDO-60°=180°-60°-60°-∠BDP,推出∠PBD+∠BOP=120°-60°=60°,于是得到结论.
解答 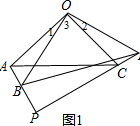 解:(1)∠APD=90°,
解:(1)∠APD=90°,
理由:∵∠1+∠3=∠2+∠3=90°,
∴∠1=∠2,
在△OAB与△ODC中,
$\left\{\begin{array}{l}{OA=OC}\\{∠1=∠2}\\{OB=OD}\end{array}\right.$,
∴△OAB≌△OCD,
∴∠OBA=∠ODC,
∴∠PBD=180°-∠ABO-∠OBD=180°-45°-∠ODC=180°-45°-45°-∠BOP=90°-∠BDP,
∴∠PBD+∠BOP=90°,
∴∠APD=180°-90°=90°.
故答案为:90°;
(2)∠APD=120°,
理由:同(1)得到∠ABO=∠CDO,
∴∠PBD=180°-∠ABO-∠OBD=180°-∠CDO-60°=180°-60°-60°-∠BDP,
∴∠PBD+∠BOP=120°-60°=60°,
∴∠APD=180°-60°=120°.
故答案为:120°.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
14.若关于x、y的多项式3nx2-x2+5x+8-(-7x2-3y+5x)的值与x无关,则n=( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |