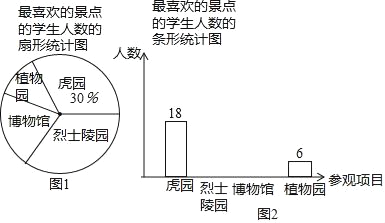
题目内容
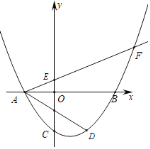
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线 ![]() 相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
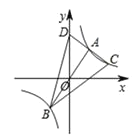
(1)k的值是________;
(2)若AD=AC,则△BCD的面积是________.
【答案】6 18
【解析】
(1)将A点横坐标代入y=![]() x求得点A坐标为(2,3),再将A点坐标代入反比例函数解析式求得k值.
x求得点A坐标为(2,3),再将A点坐标代入反比例函数解析式求得k值.
(2)依题可设点C(a,![]() ),根据中点坐标定义求得a值,从而可得C点坐标为(4,
),根据中点坐标定义求得a值,从而可得C点坐标为(4,![]() ),和D点,根据正比例函数与反比例函数交点性质可得B(-2,-3),再由B,C的坐标求出直线BC与y轴的交点,S△BAC= S△BDE+ S△BE,即可求得答案.
),和D点,根据正比例函数与反比例函数交点性质可得B(-2,-3),再由B,C的坐标求出直线BC与y轴的交点,S△BAC= S△BDE+ S△BE,即可求得答案.
解:(1)∵ A点横坐标为2, 且点A在直线y=![]() x上,
x上,
∴y=![]() ×2=3,
×2=3,
∴A(2,3),
又∵点A在反比例函数y=![]() 上,
上,
∴k=2×3=6,
故答案为:6.
(2)设点C(a,![]() ),
),
∵AD=AC,
∴点A是线段CD的中点,
∴a+0=4,
即a=4,
∴C(4,![]() ),D(0,
),D(0, ![]() )
)
∵A(2,3),直线y=![]() x与反比例函数y=
x与反比例函数y=![]() 相交于A、B两点,
相交于A、B两点,
∴B(-2,-3),
∵直线AB的解析式为:y=![]() x,
x,
直线BC的解析式为:![]() ,设BC与y轴的交点为E,则E(0,
,设BC与y轴的交点为E,则E(0,![]() ),
),
∴S△BAC= S△BDE+ S△BEC=![]() .
.
故答案为:18.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目