题目内容
12.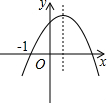 已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列三个结论:①a<0;②a+b+c>0;③-$\frac{b}{2a}$>0 ④abc>0.把正确结论的序号填在横线上①②③.
已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列三个结论:①a<0;②a+b+c>0;③-$\frac{b}{2a}$>0 ④abc>0.把正确结论的序号填在横线上①②③.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,根据对称轴在y轴的右侧可得出b的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:由抛物线的开口方向向下可推出a<0,
抛物线与y轴的正半轴相交,可得出c>0,
对称轴在y轴的右侧,a,b异号,b>0,
∴abc<0;
因为对称轴在y轴右侧,对称轴为>0;
由图象可知:当x=1时,y>0,∴a+b+c>0.
∴①,②,③都正确,
故答案为:①②③.
点评 本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定:
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.
(2)b由对称轴和a的符号确定:由对称轴公式x=-$\frac{b}{2a}$判断符号.
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.
(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.

练习册系列答案
相关题目
20.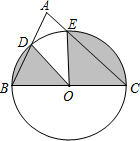 如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
 如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )| A. | $\frac{7}{18}π$ | B. | $\frac{7}{9}π$ | C. | $\frac{14}{9}π$ | D. | $\frac{28}{9}π$ |
1.若a<b,则下列各式中一定成立的是( )
| A. | a+2>b+2 | B. | a-2>b-2 | C. | -2a>-2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
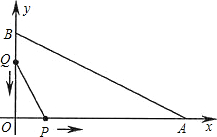 如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似? 如图,已知小强家(A)在学校(O)的南偏东50°,小华家(B)在学校的东北方向.
如图,已知小强家(A)在学校(O)的南偏东50°,小华家(B)在学校的东北方向. 如图,将一副直角三角板叠在一起,使直角顶点重合于点O,若∠AOB=160°,则∠COD=20°.
如图,将一副直角三角板叠在一起,使直角顶点重合于点O,若∠AOB=160°,则∠COD=20°.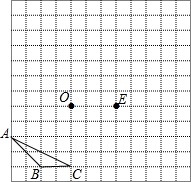 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点E、点O.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点E、点O.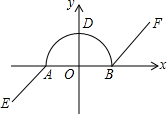 如图,在平面直角坐标系xOy中,我们把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.?当一次函数y=x+b的图象与图形C恰好只有一个公共点时,b的取值范围为b=$\sqrt{2}$或-1≤b<1;?已知?AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,则点M的横坐标x的取值范围为-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$.
如图,在平面直角坐标系xOy中,我们把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.?当一次函数y=x+b的图象与图形C恰好只有一个公共点时,b的取值范围为b=$\sqrt{2}$或-1≤b<1;?已知?AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,则点M的横坐标x的取值范围为-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$.