题目内容
17．
如图，将一副直角三角板叠在一起，使直角顶点重合于点O，若∠AOB=160°，则∠COD=20°．
分析 先根据直角三角板的性质得出∠AOC+∠DOB=180°，进而可得出∠COD的度数．
解答 解：∵△AOC△BOD是一副直角三角板，
∴∠AOC+∠DOB=180°，
∴∠AOB+∠COD=∠DOB+∠AOD+∠COD=∠DOB+∠AOC=90°+90°=180°，
∵∠AOB=160°，
∴∠COD=180°-∠AOB=180°-160°=20°．
故答案为：20°．
点评 本题考查的是角的计算，熟知直角三角板的特点是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
7．下列各数中，有理数是（ ）
| A． | $\sqrt{5}$ | B． | $\frac{π}{3}$ | ||
| C． | $\frac{1}{2}$ | D． | 3.03003000300003… |
8．比较2$\sqrt{2}$，3，$\sqrt{7}$的大小，正确的是（ ）
| A． | $\sqrt{7}$＜3＜2$\sqrt{2}$ | B． | 2$\sqrt{2}$＜$\sqrt{7}$＜3 | C． | $\sqrt{7}$＜2$\sqrt{2}$＜3 | D． | 2$\sqrt{2}$＜3＜$\sqrt{7}$ |
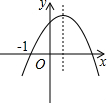已知抛物线y=ax2+bx+c（a≠0）经过点（-1，0），且顶点在第一象限．有下列三个结论：①a＜0；②a+b+c＞0；③-$\frac{b}{2a}$＞0 ④abc＞0．把正确结论的序号填在横线上①②③．
9．等腰三角形的一个内角是50°，它的一腰上的高与底边的夹角是（ ）
| A． | 25°或40° | B． | 40° | C． | 25° | D． | 65° |
