题目内容
如果一条抛物线 与
与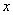 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶 点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶 点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线 的“抛物线三角形”是直角三角形,求
的“抛物线三角形”是直角三角形,求 的值;
的值;
(3)若抛物线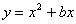 与x轴交与原点O和点B,抛物线的顶点坐标为A,△
与x轴交与原点O和点B,抛物线的顶点坐标为A,△ 是的“抛物线三角形”,是否存在以原点
是的“抛物线三角形”,是否存在以原点 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
(1)“抛物线三角形”一定是 等腰 三角形; ……………………1分
(2)(图略)
∵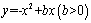 的“抛物线三角形”是直角三角形,
的“抛物线三角形”是直角三角形,
∴此“物线三角形”是等腰直角三角形,抛物线的顶点坐标为(b,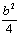 ),
),
把y=0代入得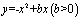 解得x=0或b
解得x=0或b
根据题意得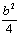 =
=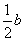
∴b=0或2(0舍去)
∴b=2 ……………………3分
(3)存在.
当b<0时,作AH⊥OB于H点,如图,
把y=0代入y=x2+bx得解得x1=0,x2=-b′,
∴B点坐标为(-b′,0),
∴A点坐标为(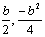 )
)
∵矩形ABCD以原点O为对称中心,
∴OA=OB=OC=OD,
∴△OAB为等边三角形,
∴AH=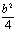
解得b1′=0,b2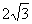
∴A点坐标为( ,-3),B点坐标为(
,-3),B点坐标为(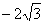 ,0)
,0)
∴C点坐标为(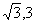 ),D点坐标为(
),D点坐标为(
设过O、C、D三点的抛物线的解析式为y=ax(x-2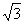 ),
),
把C(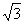 ,3)代入得a=-1,
,3)代入得a=-1,
∴所求抛物线的表达式为y=-x2+2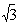
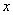 ……………………5分
……………………5分
同理,当b>0时,y=-x2-2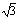
 ……………………3分
……………………3分

练习册系列答案
相关题目
 ,
, ,则对于下列结论:①
,则对于下列结论:① ②
② ∥
∥ ③
③ ,其中正确的结论有_______(把正确的结论序号全部都写上).
,其中正确的结论有_______(把正确的结论序号全部都写上).
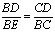 ; ③点F是BC的中点;④若
; ③点F是BC的中点;④若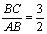 , tanE=
, tanE=

 B.
B. C.
C. D.
D.
 B.
B. C.
C.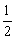 D.
D.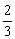
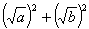 =
=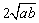 +
+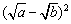 +
+ 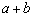 ≥
≥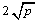 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值
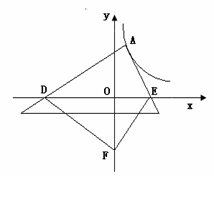
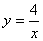 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.