题目内容
19.已知$\sqrt{15+{x}^{2}}$-$\sqrt{19-{x}^{2}}$=2,则$\sqrt{19-{x}^{2}}$•$\sqrt{15+{x}^{2}}$=15.分析 把$\sqrt{15+{x}^{2}}$-$\sqrt{19-{x}^{2}}$=2两边平方即可求解.
解答 解:∵$\sqrt{15+{x}^{2}}$-$\sqrt{19-{x}^{2}}$=2,
∴($\sqrt{15+{x}^{2}}$-$\sqrt{19-{x}^{2}}$)2=4,即15+x2+19-x2-2$\sqrt{19-{x}^{2}}$•$\sqrt{15+{x}^{2}}$=4,
∴34-2$\sqrt{19-{x}^{2}}$•$\sqrt{15+{x}^{2}}$=4,
∴$\sqrt{19-{x}^{2}}$•$\sqrt{15+{x}^{2}}$=15.
故答案是:15.
点评 本题考查了二次根式的化简求值,理解已知的式子中两个根式的被开方数的和中不含有x是关键.

练习册系列答案
相关题目
4. 在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )度.
在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )度.
 在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )度.
在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )度.| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
11.若关于x的方程3x+5k-4=0的解是x=-2,则k的值是( )
| A. | $\frac{2}{5}$ | B. | -$\frac{3}{5}$ | C. | 2 | D. | -2 |
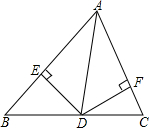 如图,在△ABC中,∠BAC=60°,点D是BC边上一点,连接AD,过点D分别作DE⊥AB于E,DF⊥AC于F.若AD=10,且DE=DF,则DE的长为5.
如图,在△ABC中,∠BAC=60°,点D是BC边上一点,连接AD,过点D分别作DE⊥AB于E,DF⊥AC于F.若AD=10,且DE=DF,则DE的长为5.