题目内容
 如图,在△ABC中,∠B=60°,∠C=54°,AD平分∠BAC交BC于D.
如图,在△ABC中,∠B=60°,∠C=54°,AD平分∠BAC交BC于D.(1)求∠ADB,∠ADC的度数;
(2)若DE⊥AC于E,求∠ADE的度数.
考点:三角形内角和定理
专题:计算题
分析:(1)先根据三角形内角和定理计算出∠BAC=180°-∠B-∠C=66°,再根据角平分线的定义得到∠BAD=∠CAD=
∠BAC=33°,然后根据三角形外角性质计算∠ADB,∠ADC的度数;
(2)利用垂直得到∠AED=90°,然后根据互余计算∠ADE的度数.
| 1 |
| 2 |
(2)利用垂直得到∠AED=90°,然后根据互余计算∠ADE的度数.
解答:解:(1)∵∠B=60°,∠C=54°,
∴∠BAC=180°-∠B-∠C=66°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=
∠BAC=33°,
∴∠ADB=∠C+∠CAD=54°+33°=87°;
∠ADC=∠B+∠CAD=60°+33°=93°;
(2)∵DE⊥AC于E,
∴∠AED=90°,
∴∠ADE=90°-∠DAE=90°-33°=57°.
∴∠BAC=180°-∠B-∠C=66°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=
| 1 |
| 2 |
∴∠ADB=∠C+∠CAD=54°+33°=87°;
∠ADC=∠B+∠CAD=60°+33°=93°;
(2)∵DE⊥AC于E,
∴∠AED=90°,
∴∠ADE=90°-∠DAE=90°-33°=57°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形的外角性质.

练习册系列答案
相关题目
下列说法中,正确的是( )
A、
| ||
| B、a是单项式,它的系数是1,次数也是1 | ||
| C、-8是单项式,它的次数是1次 | ||
| D、多项式3x2-2x-1的项是3x2,2x,1 |
小颖按如图所示的程序输入一个正整数x,最后输出的结果为656,则满足条件的x的不同值有( )个.


| A、1 | B、2 | C、3 | D、4 |
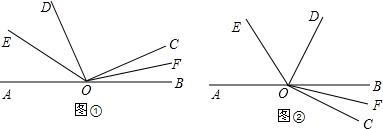
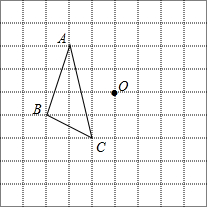 如图,三角形ABC是格点三角形(点A、B、C都在格点上),点O也在格点上.
如图,三角形ABC是格点三角形(点A、B、C都在格点上),点O也在格点上. 已知二次函数y=-x2+4x+5,完成下列各题:
已知二次函数y=-x2+4x+5,完成下列各题: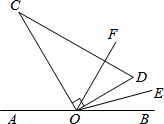 如图,点O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.已知∠AOC的度数比∠BOD的度数的3倍多10度.
如图,点O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.已知∠AOC的度数比∠BOD的度数的3倍多10度. 如图,在⊙0中,
如图,在⊙0中,