题目内容
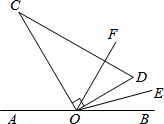 如图,点O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.已知∠AOC的度数比∠BOD的度数的3倍多10度.
如图,点O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.已知∠AOC的度数比∠BOD的度数的3倍多10度.(1)求∠BOD的度数.
(2)若OE、OF分别平分∠BOD、∠BOC,求∠EOF的度数.(写出必要的推理过程)
考点:角的计算,角平分线的定义
专题:
分析:(1)首先设∠BOD=x°,由∠AOC的度数比∠BOD的度数的3倍多10度,且∠COD=90°,可得方程:x+(3x+10)+90=180,解此方程即可求得答案;
(2)由OE、OF分别平分∠BOD、∠BOC,可得∠BOE=
∠BOD,∠BOF=
∠BOC=
(∠BOD+∠COD),又由∠EOF=∠BOF-∠BOE=
∠COD,即可求得答案.
(2)由OE、OF分别平分∠BOD、∠BOC,可得∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)设∠BOD=x°,
∵∠AOC的度数比∠BOD的度数的3倍多10度,且∠COD=90°,
∴x+(3x+10)+90=180,
解得:x=20,
∴∠BOD=20°;
(2)∵OE、OF分别平分∠BOD、∠BOC,
∴∠BOE=
∠BOD,∠BOF=
∠BOC=
(∠BOD+∠COD),
∴∠EOF=∠BOF-∠BOE=
∠COD=45°.
∵∠AOC的度数比∠BOD的度数的3倍多10度,且∠COD=90°,
∴x+(3x+10)+90=180,
解得:x=20,
∴∠BOD=20°;
(2)∵OE、OF分别平分∠BOD、∠BOC,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠BOF-∠BOE=
| 1 |
| 2 |
点评:此题考查了角的计算与角平分线的定义.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
若3x+2与x-1的值互为相反数,则( )
A、x=-
| ||
| B、x=-4 | ||
C、x=-
| ||
D、x=-
|
 如图,在△ABC中,∠B=60°,∠C=54°,AD平分∠BAC交BC于D.
如图,在△ABC中,∠B=60°,∠C=54°,AD平分∠BAC交BC于D.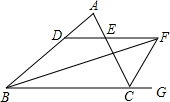 如图所示:∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.问:
如图所示:∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.问: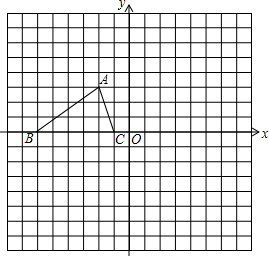 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).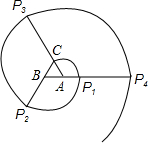 如图,正△ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4,….设ln为扇形Dn的弧长(n=1,2,3,…),Sn为扇形Dn的面积.
如图,正△ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4,….设ln为扇形Dn的弧长(n=1,2,3,…),Sn为扇形Dn的面积.