Question

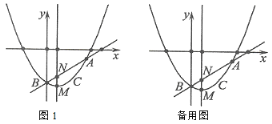
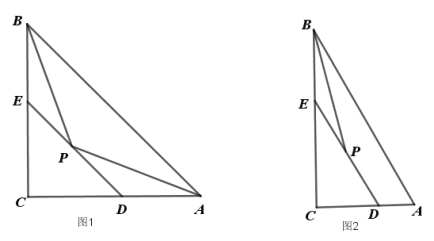
【题目】（1）如图1．在Rt△ABC中，∠C=90°，AC=BC，AP、BP分别平分∠CAB、∠CBA，过点P作DE∥AB交AC于点D，交BC于点E．求证：①点P是线段DE的中点；②求证：BP2=BE·BA；

（2）如图2．在Rt△ABC中，∠C=90°，AB=13，BC=12，BP平分∠ABC，过点P作DE∥AB交AC于点D，交BC于点E，若点P为线段DE的中点，求AD的长度．

Answer 1

【答案】（1）①见解析，②见解析；（2）

【解析】

（1）①由角平分线的性质和平行线的性质得到，根据等角对等边得到EB=PE，同理得到AD=DP．由平行线分线段成比例定理得到，进而得到EP=DP，即可得出结论；

②先证，由相似三角形对应边成比例得到，即可得出结论；

（2）根据勾股定理，得到AC的长．由（1）得．设AD=x，则，设AD=x，则．有平行线分线段成比例定理可求出BE的长，进而得到CE、DE的长．在Rt△CDE中，根据勾股定理即可得到结论．

（1）①证明：∵平分，

∴．

∵，

∴，

∴，

∴，

同理．

∵，

∴，

∵，

∴，

∴，即，

∴，

∴是的中点；

②由①得，

∵平分，

∴．

∵，

∴，

∴，

∴，

∴，

∴；

（2）由勾股定理，得：．

由（1）得．

设AD=x，则．

∵，

∴，

∴，

∴BE=，

∴EP=PD=BE=，，

∴DE=．

在Rt△CDE中，∵，

∴，解得：，或(不合题意，舍去)．故AD的长为．