Question

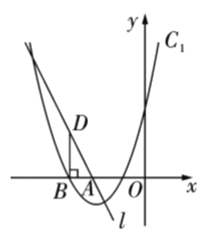
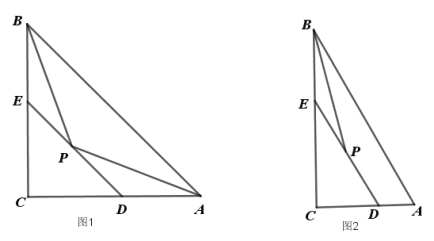
【题目】如图1，抛物线过点，，点为直线下方抛物线上一动点，为抛物线顶点，抛物线对称轴与直线交于点．

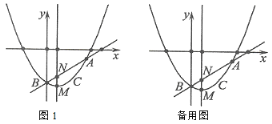
（1）求抛物线的表达式与顶点的坐标；

（2）在直线上是否存在点，使得，，，为顶点的四边形是平行四边形，若存在，请求出点坐标；

（3）在轴上是否存在点，使？若存在，求点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1），点的坐标为（1，－4）；（2）符合条件的点的坐标为，；（3）点的坐标为或．

【解析】

（1），代入抛物线即可求出抛物线解析式，配方即可求出顶点坐标；

（2）用待定系数法求出直线的表达式为，求得MN=1，分①若为平行四边形的一边，则有，且及②若为平行四边形的对角线，进行解答即可；

（3）构造,使得，作轴，则，根据勾股定理可得，即可求出点的坐标

（1）把，代入抛物线得

解得：

∴

∵

∴点的坐标为（1，－4）．

（2）设直线的表达式为，则

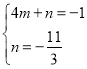
解得：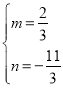

∴直线的表达式为．

当时，，

∴点的坐标为（1，－3），

∴．

①若为平行四边形的一边，则有，且．

设点坐标，则，

∴，

∴（舍去），．

∴点坐标为．

②若为平行四边形的对角线，设，则．

代入抛物线得：，解得（舍去），，

∴

综上所述，符合条件的点的坐标为，．

（3）

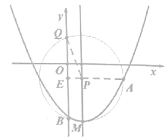
如图，在对称轴上取点，易得，且，以为圆心，为半径作圆交轴与点，则．作轴，则，

又∵，

∴

∴点的坐标为或．