Question

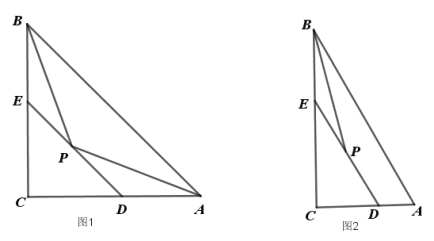
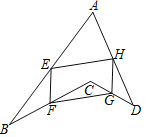
【题目】如图，在“飞镖形”ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点．

（1）求证：四边形EFGH是平行四边形；

（2）“飞镖形”ABCD满足条件　 　时，四边形EFGH是菱形．

Answer 1

【答案】(1)见解析；（2）AC=BD

【解析】

（1）连接AC，根据三角形的中位线定理求出EH＝BD，HG＝AC，EH∥BD，HG∥AC，FG∥BD，EF∥AC，推出平行四边形EFGH即可；

（2）根据菱形的判定定理即可得到结论．

（1）证明：连接AC．

∵E、F、G、H分别是AB、BC、CD、AD的中点．

∴EF、GH分别是△ABC、△ACD的中位线．

∴EF∥AC，EF＝AC，GH∥AC，GH＝AC，

∴EF＝GH，EF∥GH，

∴四边形EFGH是平行四边形；

（2） “飞镖形”ABCD满足条件AC＝BD时，四边形EFGH是菱形AC＝BD，

故答案为：AC＝BD．