Question

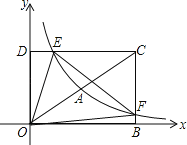
【题目】如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）．若反比例函数（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F．设直线EF的解析式为y2=k2x+b．

（1）求反比例函数和直线EF的解析式；

（温馨提示：平面上有任意两点M（x1，y1）、N（x2，y2），它们连线的中点P的坐标为（ ））（2）求△OEF的面积；

（3）请结合图象直接写出不等式k2x -b﹣＞0的解集．

Answer 1

【答案】（1）（2）（3）x＜-6或-1.5＜x＜0

【解析】

（1）根据点A是OC的中点，可得A（3，2），可得反比例函数解析式为y1=，根据E（，4），F（6，1），运用待定系数法即可得到直线EF的解析式为y=-x+5；

（2）过点E作EG⊥OB于G，根据点E，F都在反比例函数y1=的图象上，可得S△EOG=S△OBF，再根据S△EOF=S梯形EFBG进行计算即可；

（3）根据点E，F关于原点对称的点的坐标分别为（-1.5，-4），（-6，-1），可得不等式k2x-b-＞0的解集为：x＜-6或-1.5＜x＜0．

（1）∵D（0，4），B（6，0），

∴C（6，4），

∵点A是OC的中点，

∴A（3，2），

把A（3，2）代入反比例函数y1=，可得k1=6，

∴反比例函数解析式为y1=，

把x=6代入y1=，可得y=1，则F（6，1），

把y=4代入y1=，可得x=，则E（，4），

把E（，4），F（6，1）代入y2=k2x+b，可得

，解得，

∴直线EF的解析式为y=-x+5；

（2）如图，过点E作EG⊥OB于G，

∵点E，F都在反比例函数y1=的图象上，

∴S△EOG=S△OBF，

∴S△EOF=S梯形EFBG=（1+4）×=；

（3）由图象可得，点E，F关于原点对称的点的坐标分别为（-1.5，-4），（-6，-1），

∴由图象可得，不等式k2x-b-＞0的解集为：x＜-6或-1.5＜x＜0．